实际单相变压器的电压比
理想变压器只存在于理论之中。我们在实际生活中能用得着的,还是实际变压器。
实际变压器的特性与理想变压器很相似,但也只是相似,并不完全相同。
感应电动势
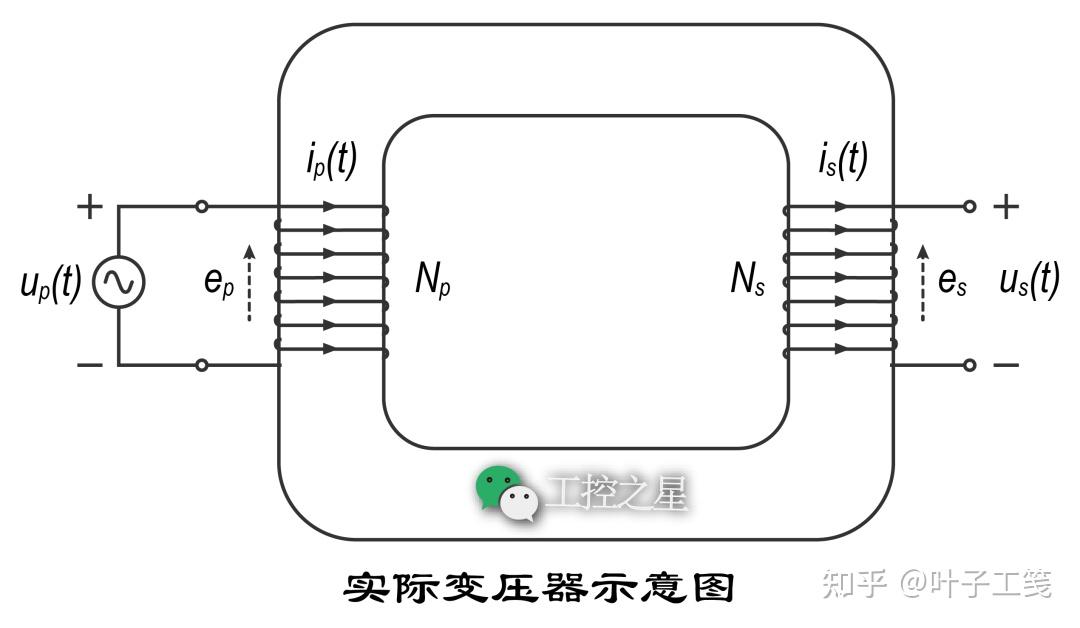
假设图中是一个实际变压器的示意图。变压器中一次绕组的匝数是 Np,二次绕组的匝数是 \(N_{s}\)。一次绕组的两端连接了交流电源,交流电源的电压为 \(u_{p}(t)\)。二次绕组的两端保持开路。
根据法拉第的电磁感应定律,感应电动势和绕组的全磁通(也叫磁通匝链数)之间的关系如下:
\[
\begin{align*}
e_{ind} = \frac{\mathrm{d}\lambda}{\mathrm{d}t}
\end{align*}
\]
其中,全磁通 (λ) 是通过绕组中每匝线圈的磁通量之和。即:
\[
\begin{align*}
\lambda = \sum_{i=1}^{N} \, \phi_{i}
\end{align*}
\]
在理想变压器中,我们假设没有漏磁或漏磁很少(可以忽略不计),而且每匝线圈中的磁通量大致相同(均为 φ)。因此,理想变压器中通过绕组的全磁通可以简化为:
\[
\begin{align*}
\lambda = N \phi
\end{align*}
\]
但在实际变压器中,因为位置差异,每匝线圈中的磁通量都稍稍有些各不相同。上式中的全磁通简化公式,就不太适用了。
不过,我们可以定义另一个术语,叫做每匝线圈的平均磁通量。每匝线圈的平均磁通量可计算如下:
\[
\begin{align*}
\overline{\phi} = \frac{\lambda}{N}
\end{align*}
\]
其中,λ 是绕组中的全磁通,N 是绕组中的线圈匝数。
因此,法拉第的电磁感应定律就可以改写为:
\[
\begin{align*}
e_{ind} = N \frac{\mathrm{d} \overline{\phi}}{\mathrm{d}t}
\end{align*}
\]
主磁通和漏磁通
假设一次绕组的阻抗为零,绕组上每匝线圈的平均磁通量可计算如下:
\[
\begin{align*}
e_{p} &= N_p \frac{\mathrm{d}\overline{\phi_p}}{\mathrm{d}t} = u_p(t) \\
\mathrm{d}\overline{\phi_p} &= \frac{1}{N_p} u_p(t)\mathrm{d}t \\
\overline{\phi_p} &= \frac{1}{N_p} \int u_p(t)\mathrm{d}t
\end{align*}
\]
由此可见,一次绕组上每匝线圈的平均磁通量与绕组两端的交流电压的积分成正比,比例常数是一次绕组上线圈匝数的倒数 (\(1/N_{p}\))。
在实际变压器中,一次绕组中的磁通量并不会全部传递到二次绕组中。总有一部分磁通量会穿透铁芯,泄露到空气中。这部分泄露到空气中的磁通量,被称为漏磁通。留在铁芯中的磁通量,被称为主磁通。
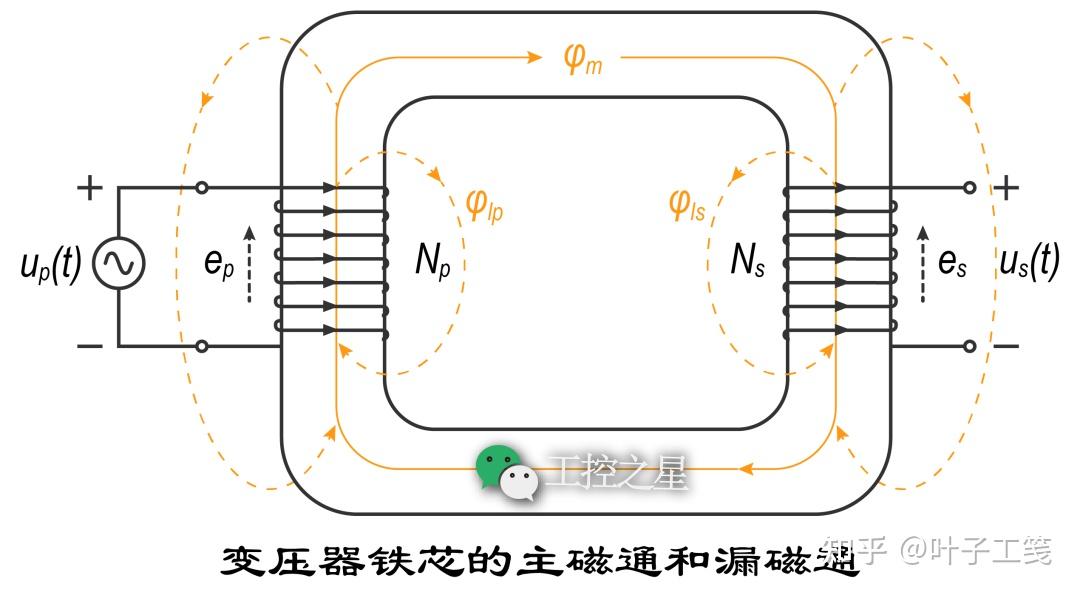
换句话说,一次绕组中每匝线圈的平均磁通量可分成两个部分:主磁通和漏磁通。主磁通的磁力线总是处于铁芯中,既穿过一次绕组,也穿过二次绕组。漏磁通的磁力线穿过一次绕组,但不穿过二次绕组,而是通过空气返回一次绕组。
\[
\begin{align*}
\overline{\phi_p} = \phi_m + \phi_{lp}
\end{align*}
\]
其中,φm 是主磁通,φlp 是一次绕组的漏磁通。
同理,二次绕组中每匝线圈的平均磁通量也分为主磁通和漏磁通。二次绕组的漏磁通,穿过一次绕组,但不穿过一次绕组,而是通过空气返回二次绕组。
\[
\begin{align*}
\overline{\phi_s} = \phi_m + \phi_{ls}
\end{align*}
\]
其中,\(φ_{m}\) 是主磁通,\(φ_{ls}\) 是二次绕组的漏磁通。
电压比
如果将每匝线圈的平均磁通量拆分成主磁通和漏磁通,一次绕组的电磁感应电动势可以拆分如下:
\[
\begin{align*}
e_{p} = u_p(t) &= N_p \frac{\mathrm{d}\overline{\phi_p}}{\mathrm{d}t} \\
&= N_p \frac{\mathrm{d}{\phi_m}}{\mathrm{d}t} + N_p \frac{\mathrm{d}{\phi_{lp}}}{\mathrm{d}t} \\
&= e_p(t) + e_{lp}(t)
\end{align*}
\]
其中,\(e_{p}(t)\) 是主磁通的变化在一次绕组中产生的感应电动势,\(e_{lp}(t)\) 是一次绕组的漏磁通变化产生的感应电动势。
同理,二次绕组中电磁感应电动势也可以拆分如下:
\[
\begin{align*}
e_{s} = u_s(t) &= N_s \frac{\mathrm{d}\overline{\phi_s}}{\mathrm{d}t} \\
&= N_s \frac{\mathrm{d}{\phi_m}}{\mathrm{d}t} + N_s \frac{\mathrm{d}{\phi_{ls}}}{\mathrm{d}t} \\
&= e_s(t) + e_{ls}(t)
\end{align*}
\]
其中,\(e_{s}(t)\) 是主磁通的变化在二次绕组中产生的感应电动势,\(e_{ls}(t)\) 是二次绕组的漏磁通变化产生的感应电动势。
主磁通的变化在一次绕组和二次绕组中产生的感应电动势分别为:
\[
\begin{align*}
e_p(t) &= N_p \frac{\mathrm{d}{\phi_m}}{\mathrm{d}t} \\
e_s(t) &= N_s \frac{\mathrm{d}{\phi_m}}{\mathrm{d}t} \\
\end{align*}
\]
由此,可以推导出以下关系式:
\[
\begin{align*}
\frac{\mathrm{d}{\phi_m}}{\mathrm{d}t} = \frac{e_p(t)}{N_p} &= \frac{e_s(t)}{N_s} \\
\frac{e_p(t)}{e_s(t)} &= \frac{N_p}{N_s} = k
\end{align*}
\]
从这个关系式可以看出,主磁通的变化在一次绕组和二次绕组中产生的感应电动势之比等于实际变压器的匝数比。
如果变压器的设计合理,不管是一次绕组还是二次绕组,主磁通都会远远大于漏磁通。所以,一次绕组和二次绕组两端的电压比也近似等于实际变压器的匝数比。而且,变压器的漏磁通越少,其电压比就越接近匝数比(即理想变压器的电压比)。
\[
\begin{equation*}
\frac{u_p(t)}{u_s(t)} \approx \frac{N_p}{N_s} = k
\end{equation*}
\]

