实际变压器的励磁电流

在介绍理想变压器的电流比时，我们提到过一个叫空载电流的术语，你还记得吗?

如果有一个理想变压器，一次绕组的两端接通交流电源，二次绕组的两端保持开路。这时，一次绕组中的电流就是空载电流。

在实际变压器中，空载电流还有另外一个名字，叫做励磁电流（或者激磁电流）。

磁化电流

假设有一个变压器，变压器的一次绕组接通了交流电源，二次绕组的两端保持开路。交流电源的电压为 \(u_{p}(t)\)，其表达式如下：

\[ u_p(t) = U_m \cos{\omega t} \]

假设一次绕组的阻抗为零，每匝线圈的平均磁通量可计算如下：

\[ \begin{align*} \overline{\phi_p} &= \frac{1}{N_p} \int u_p(t)\mathrm{d}t \\ &= \frac{1}{N_p} \int U_m \cos{\omega t}\mathrm{d}t \\ &= \frac{U_m}{\omega N_p} \sin{\omega t}\mathrm{d}t \\ \end{align*} \]

由此可以看出，每匝线圈的平均磁通量滞后于输入电压，二者之间的相位差是 90°。

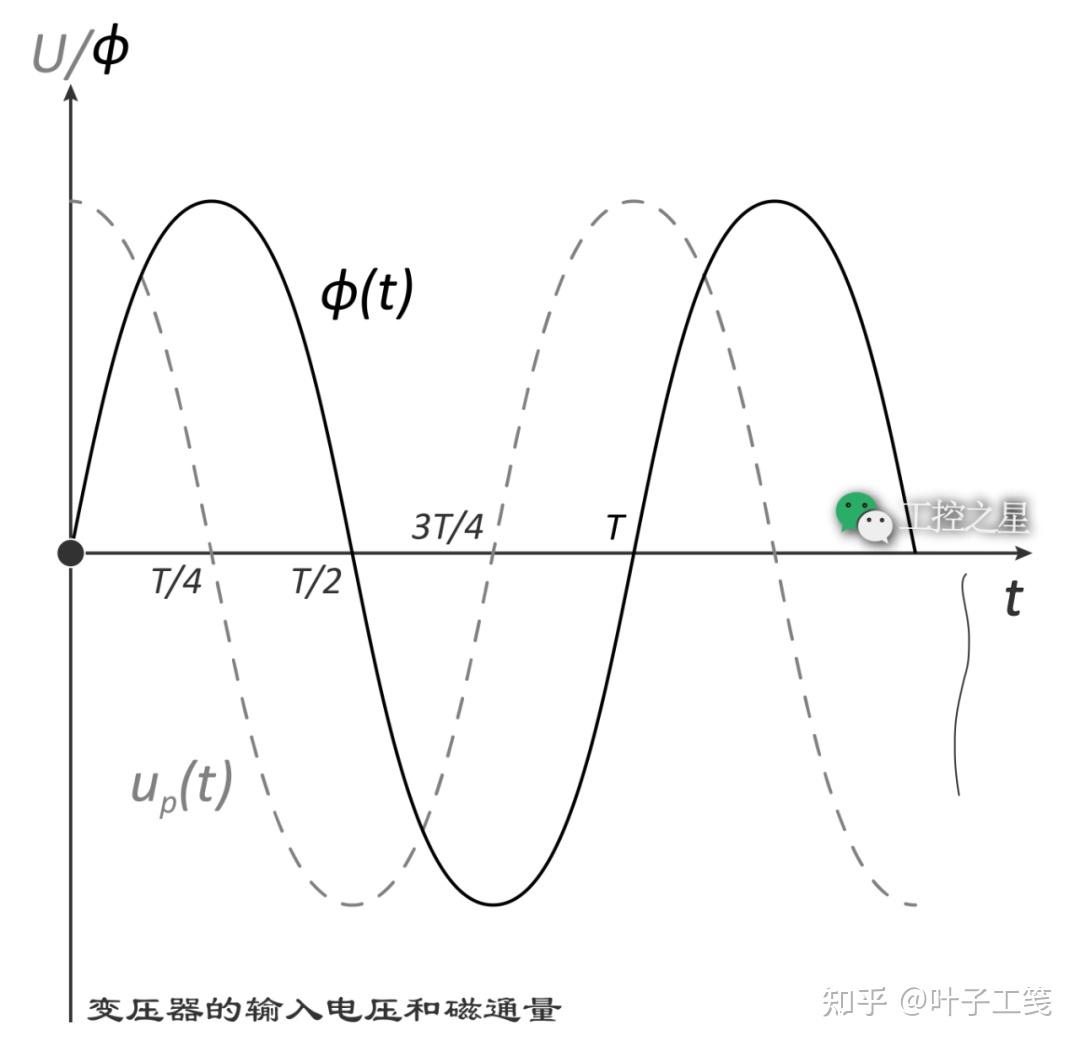
如果我们在平均磁通量曲线中均匀地采集一些数据点，就可以利用磁化曲线找出各个数据点的磁通量对应的磁动势。

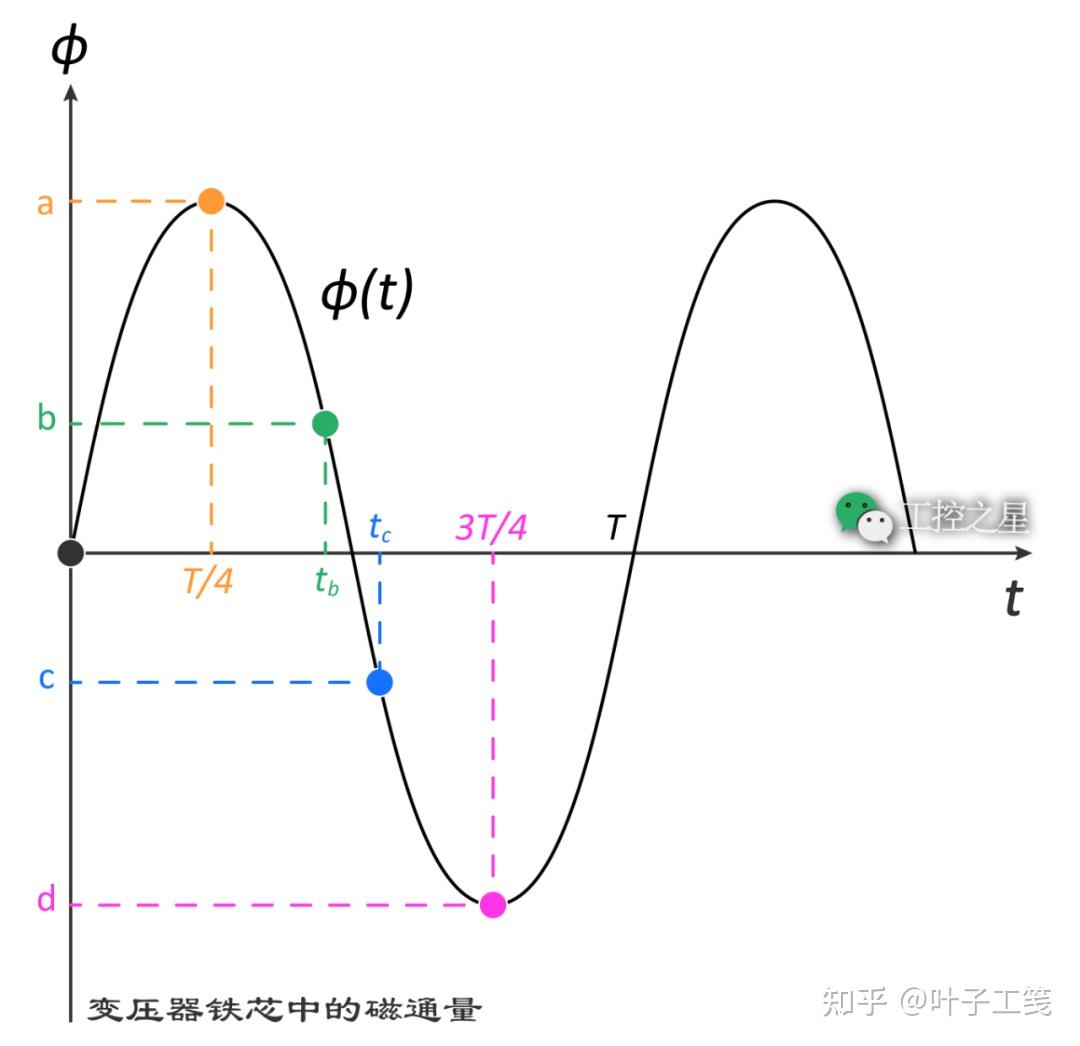
假设变压器铁芯的磁化曲线如下，纵轴是磁通量 (φ)，横轴是磁动势 (\(F_{m}\))。根据各个数据点的磁通量，找出对应的磁动势如下：

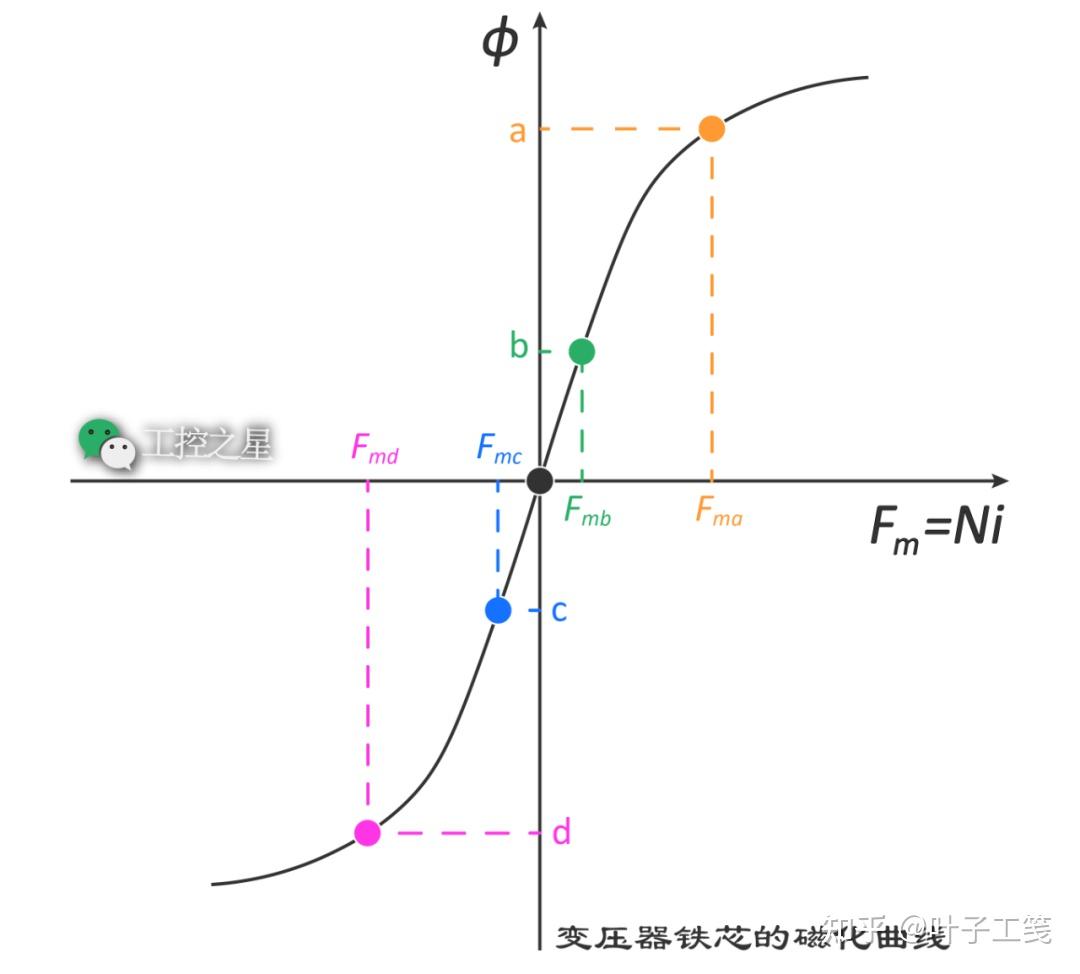
根据磁动势的计算公式 (\(F_{m} = Ni\))，我们可以很轻松地计算出各个数据点的磁化电流。如果以时间为横轴、以磁化电流为纵轴绘制一条曲线(也就是将平均磁通量曲线中的纵轴改为磁化电流)，就可以绘制出磁化电流随时间变化的曲线如下：

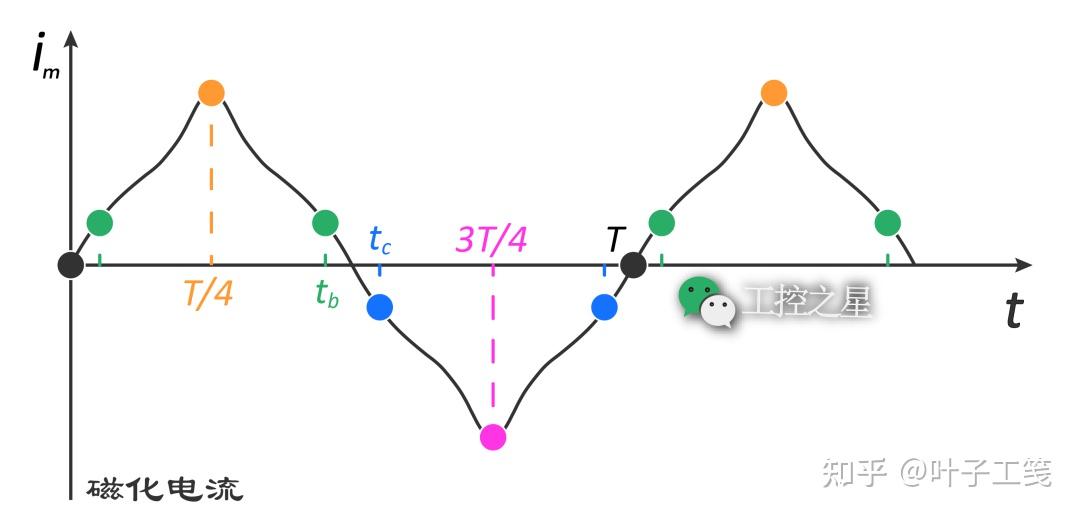
从磁化电流曲线可以看出，磁化电流并不是正弦波。当变压器铁芯中的磁通量没有达到磁化曲线的膝点时（即磁路处于非饱和区），磁化电流随时间呈正弦变化。当变压器铁芯中的磁通量超过磁化曲线的膝点之后（即磁路逐渐饱和），继续增大磁通量需要的磁化电流就不再是等比的增幅，而是越来越大的增幅，磁化电流曲线就会变成尖顶波。而且，变压器铁芯中的磁通量越饱和，磁化电流的波形就越尖。

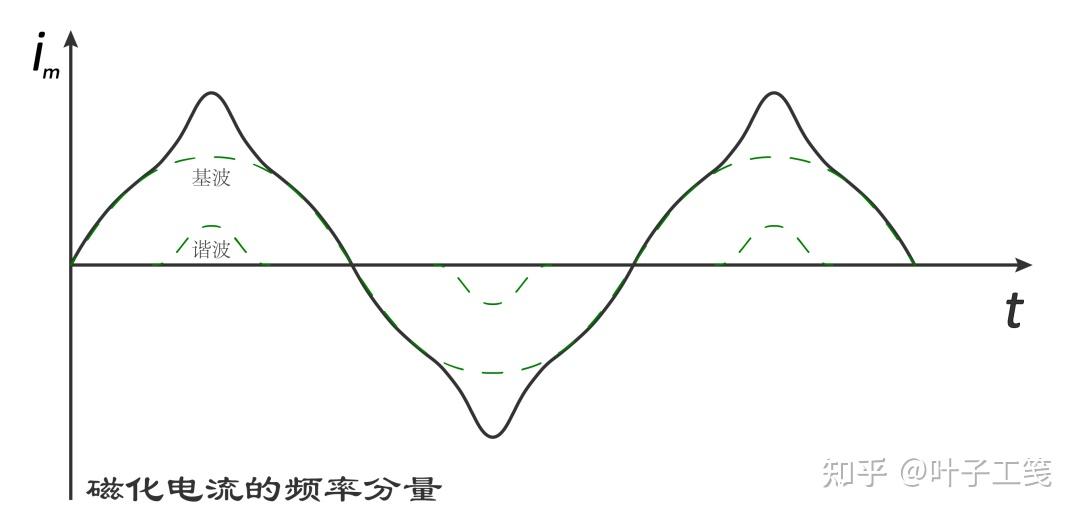
磁化电流的频率分量

傅里叶级数可以将任意周期函数分解为无数个正弦函数或余弦函数的代数和。这些正弦函数或余弦函数的角频率都是原周期函数角频率的整数倍。

其中，角频率和原周期函数相同的正弦函数（或余弦函数）叫做基波，其他函数叫做谐波。

如果将磁化电流随时间变化的曲线展开为傅里叶级数，那么：

• 基波分量的频率和相位与平均磁通量曲线完全相同，但滞后于变压器的输入电压 90°。
• 谐波分量可能比基波分量大很多。通常，变压器铁芯中的磁通量越饱和，谐波分量就越大。

铁耗电流

实际变压器工作时，铁芯中总是会产生磁滞损耗和涡流损耗。用来补偿这部分损耗的电流，叫做铁耗电流。

涡流损耗是由于铁芯中的磁通量变化使自身产生感应电动势，进而引起涡流，从而造成的热量损失。涡流的大小与铁芯中磁通量的变化率成正比。

假设铁芯中的磁通量随时间变化的曲线是一个正弦函数，那么磁通量变化率最大的位置就是磁通量为零的时候。也就是说，当铁芯中的磁通量为零时，涡流最大，铁耗电流最大。

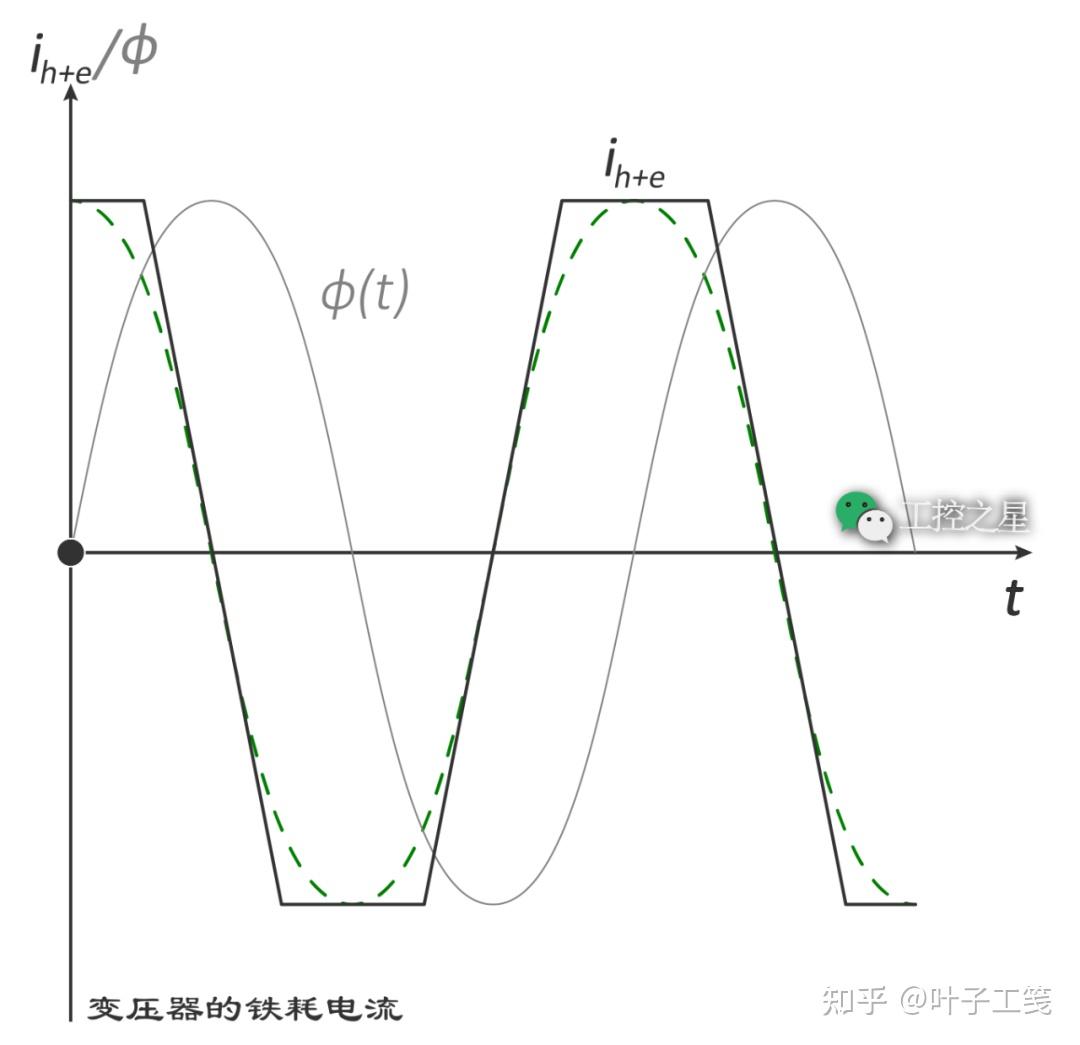
铁耗电流的两个特点如下：

• 由于磁滞损耗不是线性变化的，所以铁耗电流也不是线性变化的。
• 铁耗电流的基波分量与变压器的输入电压同相。

励磁电流

本文开头提到过，空载电流也叫励磁电流。它是磁化电流和铁损电流的总和。

\[ i_{ex} = i_m + i_{h+e} \]

其中，\(I_{m}\) 是磁化电流，\(I_{h+e}\) 是铁损电流。

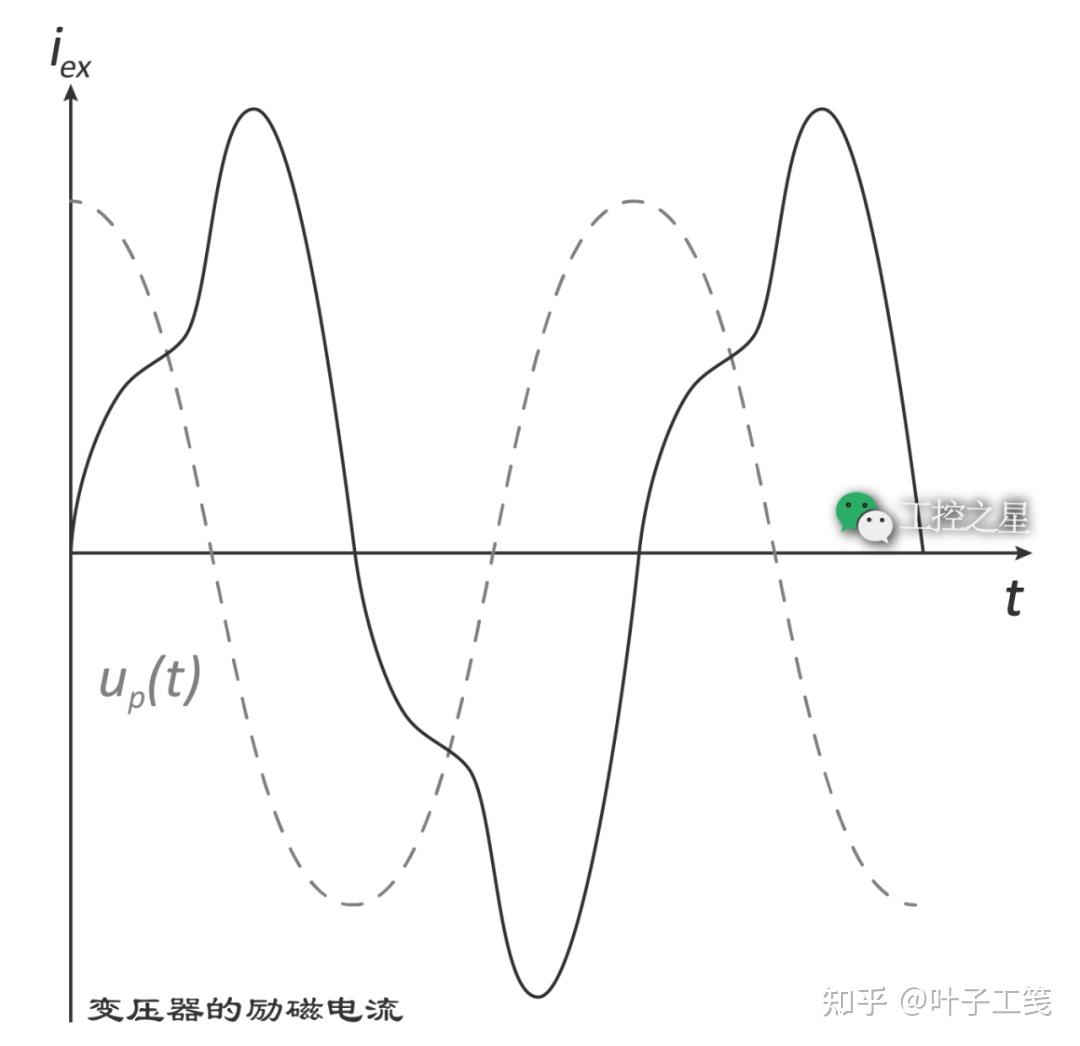
如果变压器的设计合理，励磁电流会远远小于满载电流。