标幺值

分析含有变压器的电路是一件很烦苦的工作。即使是近似等效电路和简化等效电路，也绕不过那烦人的绕组归算。

但有一种方法可以巧妙地化解这个难题，不但可以帮用户躲过绕组归算的苦累，还顺带降低了出错的几率。注意我说的是“帮用户”躲过，不是帮所有人躲过哦！毕竟难题是不会凭空消失的！

那么那个苦累的差事被谁捡走了呢? 就是这个方法本身：标幺值！

标幺值的定义

标幺值是指某一物理量的实际值与基值之比。

\[ 标幺值 = \dfrac{实际值}{基值} \]

其中，实际值是指按某种单位制（比如伏特、安培和欧姆等）测量和计算出的实际值，基值是指根据需要选择的基准值。

选择基值

计算标幺值之前，先要选择合适的基值。进行电路分析时，通常先为电压和功率（视在功率）选择基值，然后利用电路的基本定律推导出其他物理量的基值。

不过，先为哪两个物理量选择基值，你其实可以随便定。比如，先为电压和电流选择基值，然后利用电路的基本定律推导出其他物理量的基值。

在单相交流电路中，假设先将电压和电流的基值定为 \(U_{b}\) 和 \(I_{b}\)。则视在功率、阻抗和导纳的基值可以计算如下：

\[ \begin{align*} S_{b} &= U_{b}I_{b} \\ Z_{b} &= \dfrac{U_{b}}{I_{b}} \\ Y_{b} &= \dfrac{I_{b}}{U_{b}} \\ \end{align*} \]

假设先将视在功率和电压的基值定为 \(S_{b}\) 和 \(U_{b}\)，则电流、阻抗和导纳的基值可以计算如下：

\[ \begin{align*} I_{b} &= \dfrac{S_{b}}{U_{b}} \\ Z_{b} &= \dfrac{(U_{b})^{2}}{S_{b}} \\ Y_{b} &= \dfrac{S_{b}}{(U_{b})^{2}} \\ \end{align*} \]

变压器参数的标幺值

在分析含有变压器的电路时，电压和功率的基值总是在某个特定的点上选取的（比如下图中的 a 点或 b 点）。

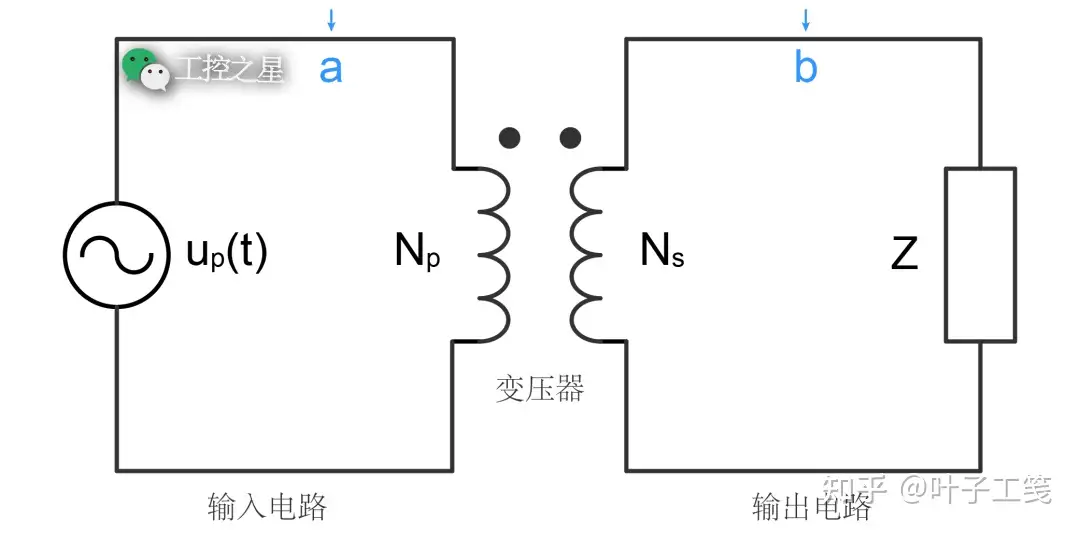
根据变压器的功率守恒原理（即变压器的输入功率等于输出功率），变压器不会改变电路中的功率大小。因此，在变压器的两侧，为功率选取的基值通常是相同的，即：

\[ \begin{align*} S_{pb} = S_{sb} \end{align*} \]

根据变压器的电压比公式，变压器的输入电压和输出电压之比等于变压器的匝数比，而变压器的匝数比约等于变压器两侧的额定电压之比。因此，在变压器的两侧，通常将各侧的额定电压作为电压的基值，即：

\[ \begin{align*} U_{pb} &= U_{pN} \\ U_{sb} &= U_{sN} \\ \dfrac{U_{pb}}{U_{sb}} &= \dfrac{U_{pN}}{U_{sN}} = k \end{align*} \]

因此，变压器的输入电压和输出电压可以用标幺值表示为：

\[ \begin{align*} U_{p,pu} &= \dfrac{U_p}{U_{pb}} \\ U_{s,pu} &= \dfrac{U_s}{U_{sb}} \\ \end{align*} \]

两式相除，可得：

\[ \begin{align*} \dfrac{U_{p,pu}}{U_{s,pu}} &= \dfrac{U_p}{U_s} \times \dfrac{U_{sb}}{U_{pb}} \\ &= k \times \dfrac{1}{k} \\ &= 1 \end{align*} \]

也就是说，如果将变压器的额定电压作为电压的基值，变压器的输入电压标幺值等于变压器的输出电压标幺值：

\[ U_{p,pu} = U_{s,pu} \]

所以，无论归算到哪一侧，变压器参数的标幺值都会保持不变。在分析包含变压器的电路时，使用标幺值就不用再进行绕组归算了。

如果一个电路中有多台变压器或电机，电压和功率的基值就可以任意选了，只要保证整个电路都使用统一的基值就行。不过，大家通常都使用容量最大的设备的额定电压和额定功率作为整个电路的基值。

为整个电路选定标准基值 (\(S_{b0}\) 和 \(U_{b0}\)) 之后，基于其他基值计算的标幺值都要换算成以标准基值计算的标幺值。进行标幺值换算时，你可以先将所有的标幺值都换算成实际值，然后再重新以标准基值重新计算标幺值。你也可以按照下面的公式直接进行换算：

\[ \begin{align*} S_{0} &= S_{1} \dfrac{S_{b1}}{S_{b0}} \\ U_{0} &= U_{1} \dfrac{U_{b1}}{U_{b0}} \\ Z_{0} &= \dfrac{(U_{0})^2}{S_{0}} \\ &= \dfrac{(U_1)^2}{S_1} \times \dfrac{(U_{b1})^2S_{b0}}{(U_{b0})^2S_{b1}} \\ &= Z_{1} \dfrac{(U_{b1})^2S_{b0}}{(U_{b0})^2S_{b1}} \end{align*} \]

标幺值的优缺点

在与变压器和电机有关的电路分析中，使用标幺值有三大优点：

简化计算过程，减少出错几率。一些原本不相等的物理量，只要选择合适的基值，就能转换成标幺值相等的物理量。例如，上文中变压器的输入电压和输出电压转换成标幺值之后，就变成了相等的物理量了。对于用户来说，不仅计算过程变得更加简单便捷，还能避免乱中出错。

便于对比不同的变压器或电机，尤其是对比对象的容量之间有较大差距时。变压器和电机的容量范围非常大，各项参数值的变化范围也很大。因此，不同变压器或电机的参数很难进行比较，但转换成标幺值之后这个问题可能就应刃而解了。

假设有个一次绕组的电抗是 0.1 欧姆。对于一台大容量的变压器来说，这个绕组的电抗可能微不足道。但对于一台小容量的变压器来说，这个绕组的电抗可能就不容小觑了。那么这个绕组的电抗到底是大还是小呢?

如果以各个变压器或电机的额定值（比如额定电压和额定功率）作为基值，将这个一次绕组的电抗转换为标幺值，它对每个变压器或电机的影响不仅立马变得显而易见，也更具可比性。

正是因为这个原因，变压器的阻抗都是以百分比标幺值的形式刻在产品铭牌上。同步电机和感应电机也是这样。

便于对计算结果进行合理性校验。无论变压器或电机的容量大小，只要以它们各自的额定值作为基值，其典型性能参数的标幺值都会落在一段很窄的数值范围内。例如，绕组的等效电阻的标幺值大约为 0.01，绕组的漏抗的标幺值通常为 0.02~0.10，激磁电抗的标幺值通常为 10~40，铁耗电阻的标幺值通常为 50~200。因此，如果计算结果超出合理范围，就知道肯定是哪里出错了。

不过，标幺值也有一个缺点，就是没有量纲，不能用量纲关系进行校验。