理想变压器的电流比、相量比和功率守恒

理想变压器的匝数比，不仅能反应电压比，也能反应电流比和相量比。

除此之外，我们还能通过这些关系式找出理想变压器的输入功率和输出功率之间的关系。

电流比

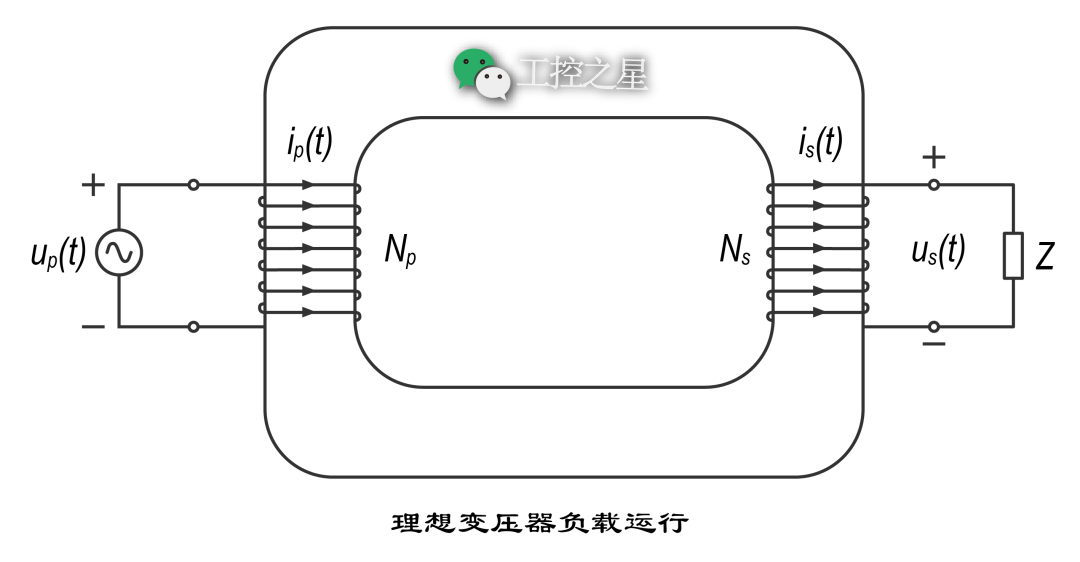
上图是理想变压器的示意图。假设一次绕组的匝数是 \(N_{p}\)，二次绕组的匝数是 \(N_{s}\)。两个绕组的缠绕方向，如图所示。

假设一次绕组的两端接通交流电源 \(u_{p}(t)\)，二次绕组两端的电压为 \(u_{s}(t)\)，铁芯中的磁通量为 φ。

如果二次绕组的两端保持开路，二次绕组中的电流为零，即空载运行。此时，一次绕组中的电流 (\(i_{0}\)) 叫做空载电流。

如果二次绕组的两端接上一个负载，就会形成闭合电路，并且电路中会产生电流。假设负载的阻抗为 Z，一次绕组中的电流为 \(i_{p}(t)\)，二次绕组中的电流为 \(i_{s}(t)\)。

理想变压器的磁路图，如下：

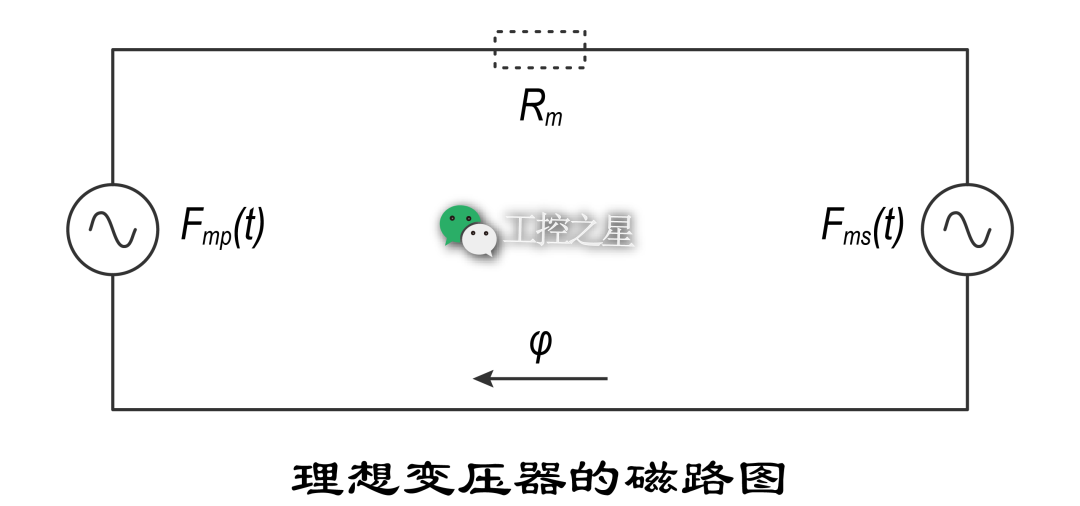
理想变压器中铁芯的磁导率无穷大，且没有漏磁，磁阻为零 (\(R_{m}=0\))。根据磁路中的欧姆定律，磁路中的磁动势可计算如下：

\[ \begin{align*} F_m(t) &= \phi R_m = 0 \\ F_m(t) &= F_{mp}(t) + F_{ms}(t) = 0 \\ \end{align*} \]

即一次绕组与二次绕组的电动势大小相等，方向相反。

\[ F_{mp}(t) = - F_{ms}(t) \]

根据安培环路定律，一次绕组和二次绕组的磁动势大小分别为：

\[ \begin{align*} F_{mp}(t) = N_{p} i_{p}(t) \\ F_{ms}(t) = N_{s} i_{s}(t) \end{align*} \]

即：

\[ \begin{align*} N_{p} i_{p}(t) &= - N_{s} i_{s}(t) \\ \frac {i_{p}(t)}{i_{s}(t)} &= - \frac{N_{s}}{N_{p}} \\ &= - \frac{1}{k} \end{align*} \]

这就是理想变压器的电流比公式。其中，k 是变压器的匝数比（也叫电压比），式中的负号表示一次绕组中的输入电流和二次绕组中的输出电流产生的磁通量方向相反。

相量比

由于一级绕组两端的输入电压和二级绕组两端的输出电压之间存在 180° 的相位差，它们的相量比公式为：

\[ \begin{equation} \frac{\dot{U_p}}{\dot{U_s}} = k\angle\pi \end{equation} \]

由于一次绕组中的输入电流和二次绕组中的输出电流产生的磁通量方向相反，它们的相量比公式为：

\[ \frac{\dot{I_p}}{\dot{I_s}} = \frac{1}{k} \angle\pi \]

功率

理想变压器的一次绕组上输入的有功功率，可计算如下：

\[ P_{in} = U_pI_p \cos \theta_p \]

理想变压器的二次绕组上输出的有功功率，可计算如下：

\[ P_{out} = U_sI_s \cos \theta_s \]

其中，\(θ_p\) 是一次绕组上的输入电压和输入电流之间的相位差，\(θ_s\) 是二次绕组上的输出电压和输出电流之间的相位差，\(U_p\)、\(U_s\)、\(I_p\) 和 \(I_s\) 是电压或电流的有效值。

根据理想变压器的相量比公式，可得：

\[ \frac{\dot{U_p}}{\dot{I_p}} = k^2\frac{\dot{U_s}}{\dot{I_s}} \]

也就是说，输入电压和输入电流之间的相位差等于输出电压和输出电流之间的相位差 (\(θ_p = θ_s = θ\))，一次绕组和二次绕组具有相同的功率因数 (cosθ)。

因此，理想变压器的输入功率和输出功率之间的关系可计算如下：

\[ \begin{align*} P_{out} &= U_sI_s\cos\theta \\ &= \frac{U_p}{k} \times kI_p \cos\theta \\ &= U_pI_p\cos\theta \\ &= P_{in} \end{align*} \]

即理想变压器的输入功率等于输出功率。

对于无功功率和视在功率，这种等值关系同样成立。

\[ \begin{align*} Q_{in} &= U_pI_p\sin\theta \\ &= U_sI_s\sin\theta \\ &= Q_{out}\\ S_{in} &= U_pI_p \\ &= U_sI_s \\ &= S_{out} \end{align*} \]