涉及理想变压器的电路分析：绕组归算

不知道你注意到没有：

变压器是利用电磁感应原理工作的。在电学上，一次绕组所在的输入电路和二次绕组所在的输出电路是两个彼此独立的电路，二者之间并没有什么直接联系。

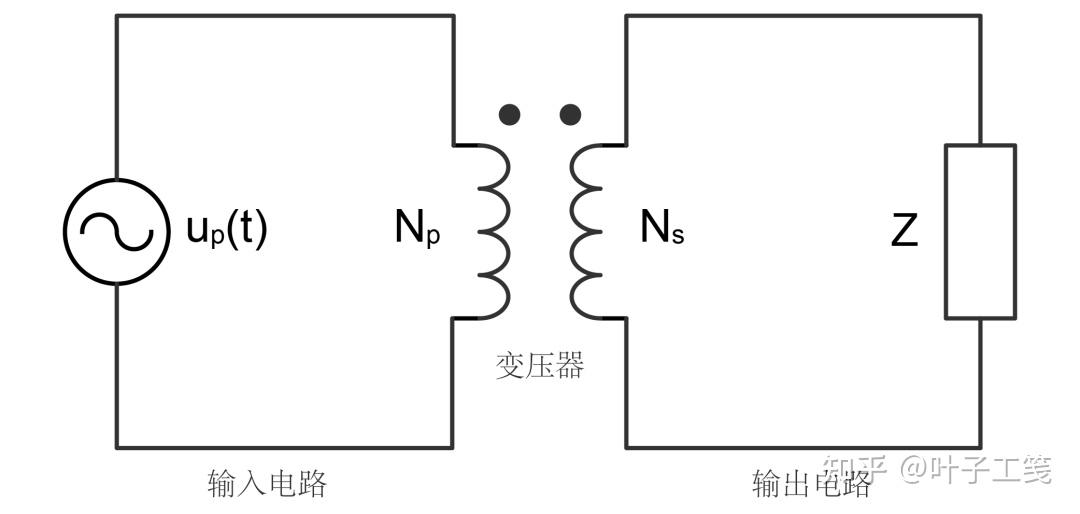
就因为这一点，如果电路中含有变压器，分析起来就会比较麻烦。为了简化分析，一般通过绕组归算的方法移除电路中的变压器，使它们重新变成只有一个电路的等效电路。

绕组归算简介

绕组归算就是通过电压比公式、电流比公式和阻抗变换公式将变压器的输入电路和输出电路转换成一个等效的单一电路。

通常情况下，变压器的输出电路会被转换到输入电路中。也可以说成是，将二次绕组归算到一次绕组。

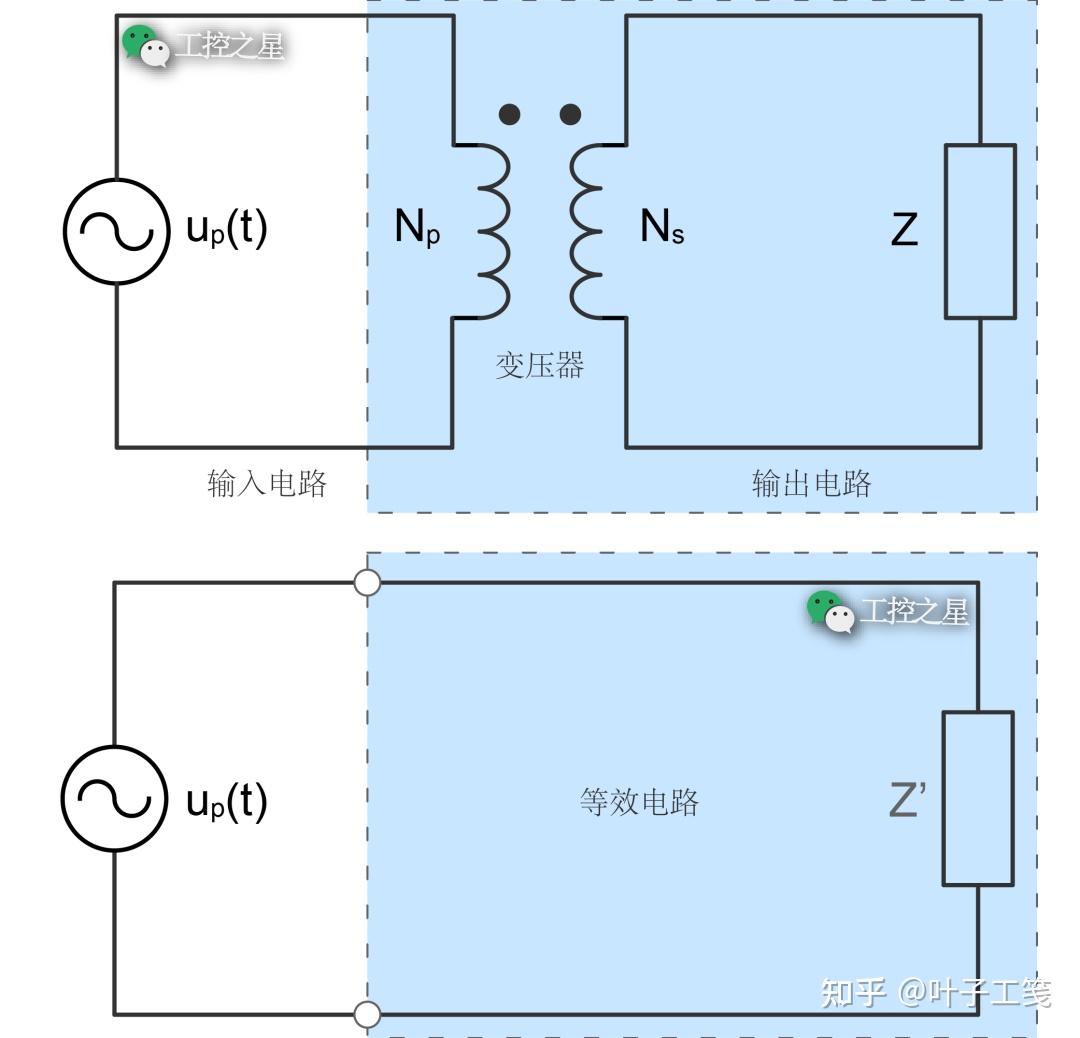
归算后的等效电路中，各物理量的值叫做归算值。假设变压器的输出电路中有一个阻抗为 Z 的负载，归算后的负载阻抗变成了 Z'，那么 Z' 就叫做 Z 的归算值。

根据理想变压器的阻抗变换公式，输出电路中负载阻抗的归算值可计算如下：

\[ \begin{equation*} Z' = k^2Z \end{equation*} \]

由于等效电路中没有变压器，我们可以按常规电路的分析方法计算电流和电压。而等效电路中的电流和电压与原电路中的实际值相等，我们再利用电压比公式或电流比公式就可以还原出变压器输出电路中的电流或电压。

示例一：直连输电

假设发电站有一台单相发电机，额定电压为 480 伏，额定频率为 50 赫兹。发电机上连接着一个阻抗为 4+3j 欧姆的负载，从发电机到负载的传输线路上有 0.18+0.24j 欧姆的阻抗。

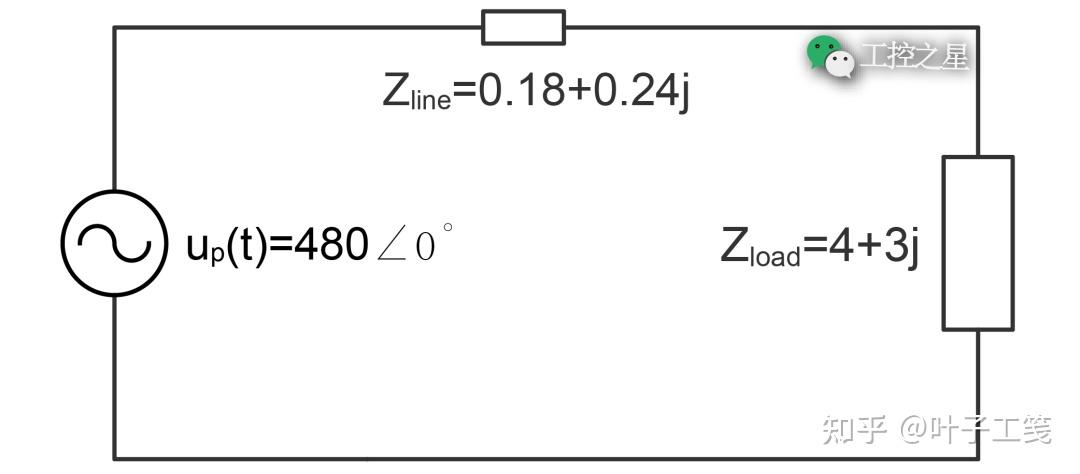
根据欧姆定律，该线路上的电流为：

\[ \begin{align*} \dot{I} &= \frac{\dot{U}_p}{Z_{line}+Z_{load}} \\ &= \frac{480 \angle{0^{\circ}}}{(0.18+0.24j)+(4+3j)} \\ &= \frac{480 \angle{0^\circ}}{4.18+3.24j} \\ &= \frac{480 \angle{0^\circ}}{5.29 \angle{37.8^\circ}} \\ &= 90.8 \angle{-37.8^\circ} \space (A) \end{align*} \]

负载两端的电压可计算如下：

\[ \begin{align*} \dot{U}_{load} &= \dot{I}Z_{load} \\ &= (90.8 \angle{-37.8^\circ})(4+3j) \\ &= (90.8 \angle{-37.8^\circ})(5 \angle{36.9^\circ}) \\ &= 454 \angle{-0.9^\circ} \space (V) \end{align*} \]

传输线路上的功率损失可计算如下：

\[ \begin{align*} P_{loss} &= I^2R_{line} \\ &= 90.8^2 \times 0.18 \\ &= 1484 \space (W) \end{align*} \]

示例二：交流输电

现在，我们在示例一的输电线路中添加两个变压器：一个是升压变压器，匝数比为 1:10，连接到发电机附近；一个是降压变压器，匝数比为 10:1，连接到负载附近。

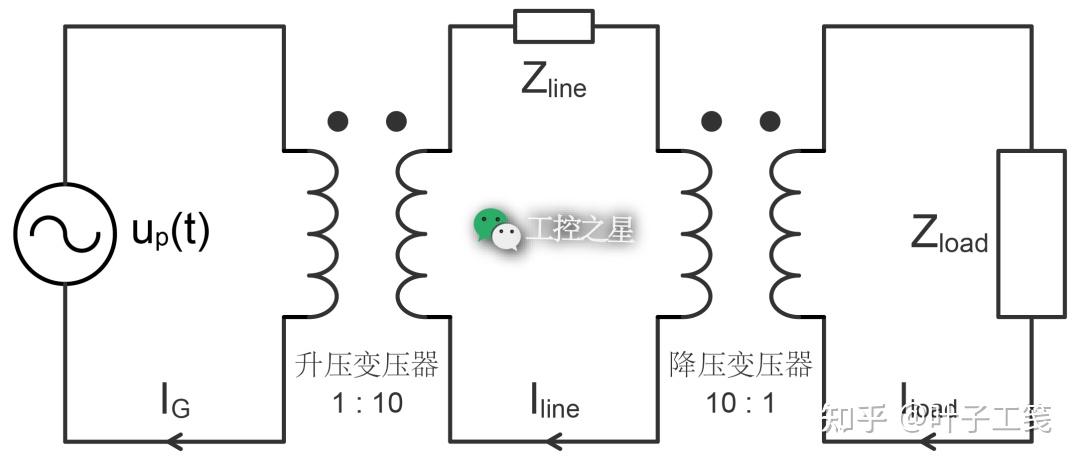
这时，我们再计算电路中的电流、负载上的电压以及传输线路中的耗损时，欧姆定律没法用了，得用本文开头介绍的绕组归算。

首先，移除电路右侧的降压变压器，将负载阻抗 (\(Z_{load}\)) 转换为降压变压器输入电路中的归算值 (\(Z'_{load}\))，然后画出它的等效电路：

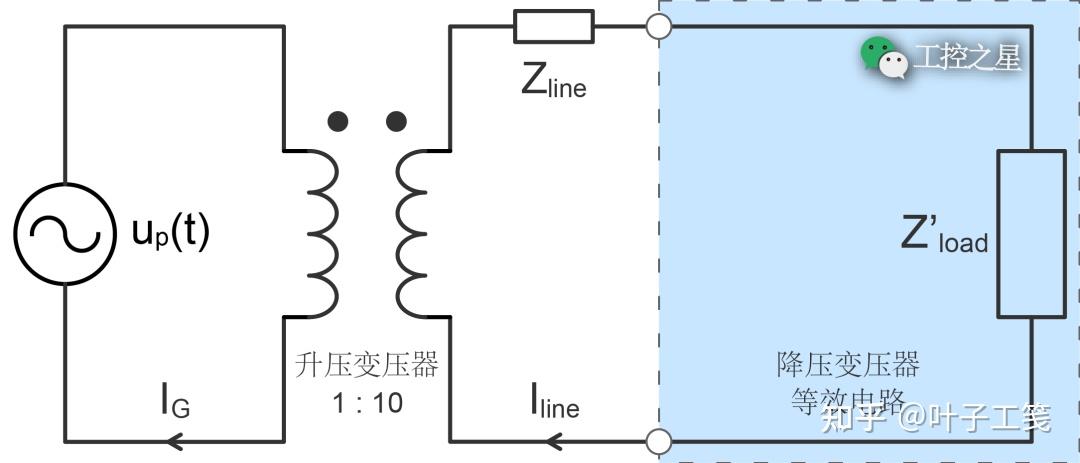
根据理想变压器的阻抗变换公式，负载阻抗的归算值可计算如下：

\[ \begin{align*} Z'_{load} &= k_2^2Z_{load} \\ &= 10^2 \times (4+3j) \\ &= 400 + 300j \space (\Omega) \end{align*} \]

接着，移除电路左侧的升压变压器，将负载阻抗的一次归算值 (\(Z'_{load}\)) 和传输线路上的阻抗 (\(Z_{line}\)) 转换为升压变压器输入电路中的归算值 (\(Z'_{line}\) 和 \(Z"_{load}\))，然后画出它的等效电路：

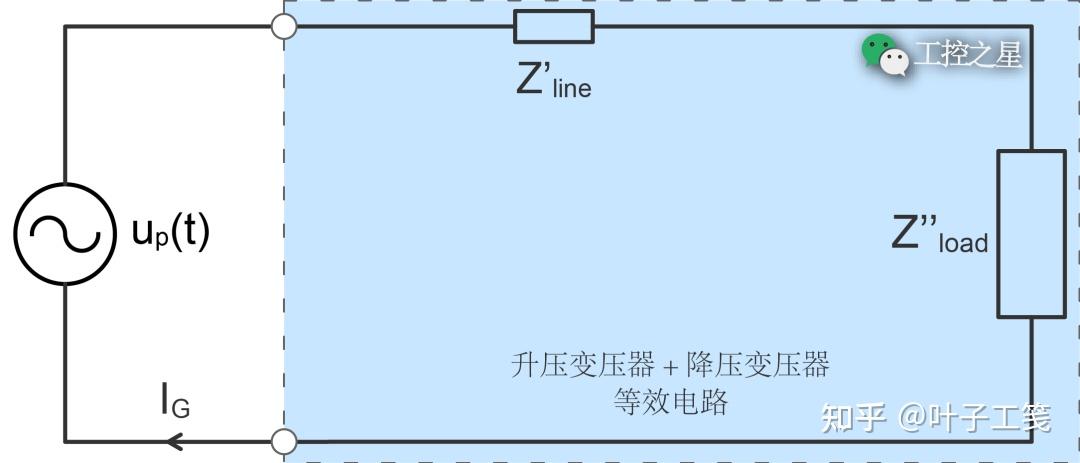
负载阻抗的二次归算值可计算如下：

\[ \begin{align*} Z"_{load} &= k_1^2Z'_{load} \\ &= \bigg(\frac{1}{10}\bigg)^2 \times (400 + 300j) \\ &= 4 + 3j \space (\Omega) \end{align*} \]

传输线路上的阻抗归算值可计算如下：

\[ \begin{align*} Z'_{line} &= k_1^2Z_{line} \\ &= \bigg(\frac{1}{10}\bigg)^2 \times (0.18 + 0.24j) \\ &= 0.0018 + 0.0024j \space (\Omega) \end{align*} \]

根据欧姆定律，发电机所在的输入电路中的电流可计算如下：

\[ \begin{align*} \dot{I}_G &= \frac{\dot{U}_p}{Z"_{load} + Z'_{line}} \\ &= \frac{480\angle{0^\circ}}{(4+3j)+(0.0018+0.0024j)} \\ &= \frac{480\angle{0^\circ}}{4.0018+3.0024j} \\ &= \frac{480\angle{0^\circ}}{5.003\angle{36.88}^\circ} \\ &= 95.94 \angle{-36.88^\circ} \space (A) \end{align*} \]

根据理想变压器的电流比公式，传输线路上的电流和负载中的电流可分别计算如下：

\[ \begin{align*} N_{p1}\dot{I}_G &= N_{s1}\dot{I}_{line} \\ \dot{I}_{line} &= \frac{N_{p1}\dot{I}_G}{N_{s1}} \\ &= \frac{1}{10} \times 95.94\angle{-36.88^\circ} \\ &= 9.594\angle{-36.88^\circ} \space (A) \\ \\ N_{p2}\dot{I}_{line} &= N_{s2}\dot{I}_{load} \\ \dot{I}_{load} &= \frac{N_{p2}\dot{I}_{line}}{N_{s2}} \\ &= 10 \times 9.594\angle{-36.88^\circ} \\ &= 95.94\angle{-36.88^\circ} \space (A) \end{align*} \]

因此，负载两端的电压可计算如下：

\[ \begin{align*} \dot{U}_{load} &= \dot{I}_{load}Z_{load} \\ &= (95.94\angle{-36.88^\circ})\times(4+3j) \\ &= (95.94\angle{-36.88^\circ})\times(5\angle{36.87^\circ}) \\ &= 479.7\angle{-0.01^\circ} \space (V) \end{align*} \]

传输线路上的功率损耗可计算如下：

\[ \begin{align*} P_{loss} &= I_{line}^2R_{line} \\ &= 9.594^2 \times 0.18 \\ &= 16.7 \space (W) \end{align*} \]

交流输电原理

发现了没有? 示例二中的电力传输损耗比示例一减少了将近 99%！这就是变压器在现代电力系统中的重要作用。

在实际的电力系统中，输电电压通常为 4~30 千伏。输电前，发电厂使用升压变压器将发电机输出的电压升高到输电电压，然后通过高压输电线将电能输送到用电地区，之后再使用降压变压器将电压降至用户需要的配电电压或用电电压。

以我国的电力系统为例，传输距离在 200~300 公里时使用 220 千伏的输电电压，传输距离在 100 公里左右时使用 110 千伏的输电电压，传输距离在 50 公里左右时使用 35 千伏或 66 千伏的输电电压。