实际变压器的T形等效电路

为了便于计算，工程上通常使用等效电路来分析实际运行中的变压器。

变压器在实际运行时主要有四种类型的损耗：铜损（热损耗）、漏磁通、铁耗（涡流损耗和磁滞损耗）和磁阻。这四种损耗也对应着理想变压器的四个假设条件。

如果将这四种主要损耗从实际变压器中分离出来，并以等效的元器件替代，那么实际变压器就可以变成一个以理想变压器和等效元器件组成的等效电路。如果利用绕组归算移除理想变压器，就可以将实际变压器转换成只有一个电路的等效电路。

铜损的等效元器件

铜损是指变压器的一次绕组和二次绕组有电流通过时由于自身电阻而产生的热损耗。

因此，一次绕组上的铜损可以等效为电阻 \(R_{p}\)，二次绕组上的铜损可以等效为电阻 \(R_{s}\)。

漏磁通的等效元器件

根据实际变压器的电压比推导公式，一次绕组上的感应电动势可以拆分为主磁通的变化产生的感应电动势和漏磁通的变化产生的感应电动势。其中，一次绕组的漏磁通变化产生的感应电动势可计算如下：

\[ e_{lp}(t) = N_p \frac{\mathrm{d}\phi_{lp}}{\mathrm{d}t} \]

同理，二次绕组的漏磁通变化产生感应电动势可计算如下：

\[ e_{ls}(t) = N_s \frac{\mathrm{d}\phi_{ls}}{\mathrm{d}t} \]

漏磁通的磁力线是通过空气返回绕组的。对于既定的变压器，空气的磁阻是恒定不变的常数，而且远远大于铁芯的磁阻。根据磁路中的欧姆定律，一次绕组中的电流与漏磁通的关系如下：

\[ \begin{align*} F_{mlp} &= N_pi_p \\ &= \phi_{lp} R_{m0} \\ &= \frac{\phi_{lp}}{\Lambda_{0}} \\ \end{align*} \]

即：

\[ \phi_{lp} = \Lambda_{0}N_pi_p \]

同理，二次绕组中的电流与漏磁通的关系如下：

\[ \phi_{ls} = \Lambda_{0}N_si_s \]

其中，\(Λ_{0}\) 是空气的磁导（即漏磁路的磁导），\(R_{m0}\) 是空气的磁阻（即漏磁路的磁阻）。

将电流与漏磁通的关系式代入漏磁通变化与感应电动势的关系式，可得：

\[ \begin{align*} e_{lp}(t) &= N_p \frac{\mathrm{d}\phi_{lp}}{\mathrm{d}t} \\ &= N_p \frac{\mathrm{d}\Lambda_{0}N_pi_p}{\mathrm{d}t} \\ &= N_p^2 \Lambda_0 \frac{\mathrm{d}i_p}{\mathrm{d}t} \\ e_{ls}(t) &= N_s \frac{\mathrm{d}\phi_{ls}}{\mathrm{d}t} \\ &= N_s \frac{\mathrm{d}\Lambda_{0}N_si_s}{\mathrm{d}t} \\ &= N_s^2 \Lambda_0 \frac{\mathrm{d}i_s}{\mathrm{d}t} \\ \end{align*} \]

如果将关系式中的常系数 \(N_{p}^2 \Lambda_{0}\) 和 \(N_{s}^2 \Lambda_{0}\) 分别使用 \(L_{p}\) 和 \(L_{s}\) 代替，上面的关系式变为：

\[ \begin{align*} e_{lp}(t) &= L_p \frac{\mathrm{d}i_p}{\mathrm{d}t} \\ e_{ls}(t) &= L_s \frac{\mathrm{d}i_s}{\mathrm{d}t} \end{align*} \]

其中，\(L_{p}\) 称为一次绕组的漏磁电感，简称漏感；\(L_{s}\) 称为二次绕组的漏感。

因此，一次绕组的漏磁通可以等效为电抗 \(X_{p}\)，二次绕组的漏磁通可以等效为电抗 \(X_{s}\)。

铁耗的等效元器件

铁芯损耗简称铁耗，是铁芯中产生的涡流损耗和磁滞损耗的总称。在实际变压器中，用于补偿铁耗的电流叫做铁耗电流。

铁耗电流与变压器的输入电压同相，而且二者的大小成正比。因此，铁耗可以等效为电阻 \(R_{c}\)。

磁阻的等效元器件

磁阻不会产生有功损耗，但会让变压器的磁化电流变大，即产生相同的主磁通所需要的磁动势变大。

磁化电流是纯无功电流，滞后于变压器的输入电压 90°。因此，磁阻可以等效为电抗 \(X_{m}\)。

绕组归算

如上所述，一个实际变压器可以等效为一个理想变压器和若干个等效元器件组成的电路，如下：

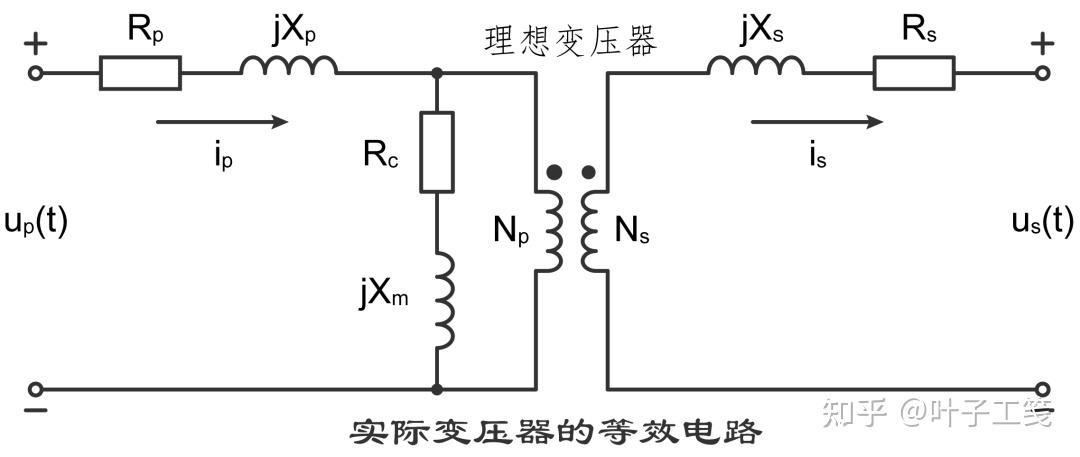
\(R_{p}\) 和 \(X_{p}\) 等效于一次绕组的铜损和漏磁通。\(R_{s}\) 和 \(X_{s}\) 等效于二次绕组的铜损和漏磁通。\(R_{c}\) 和 \(X_{m}\) 等效于铁芯的铁耗和磁阻。

其中，由 \(R_{c}\) 和 \(X_{m}\) 组成的支路叫励磁支路。励磁支路之所以放在一次绕组一侧，是因为铁芯上的电压等于变压器的输入电压减去一次绕组上的内部压降。

虽然上面的等效电路几乎等同于实际变压器，但它的用处并不大。在实际应用中，通常利用绕组归算将其转换为只有一个电路的等效电路。

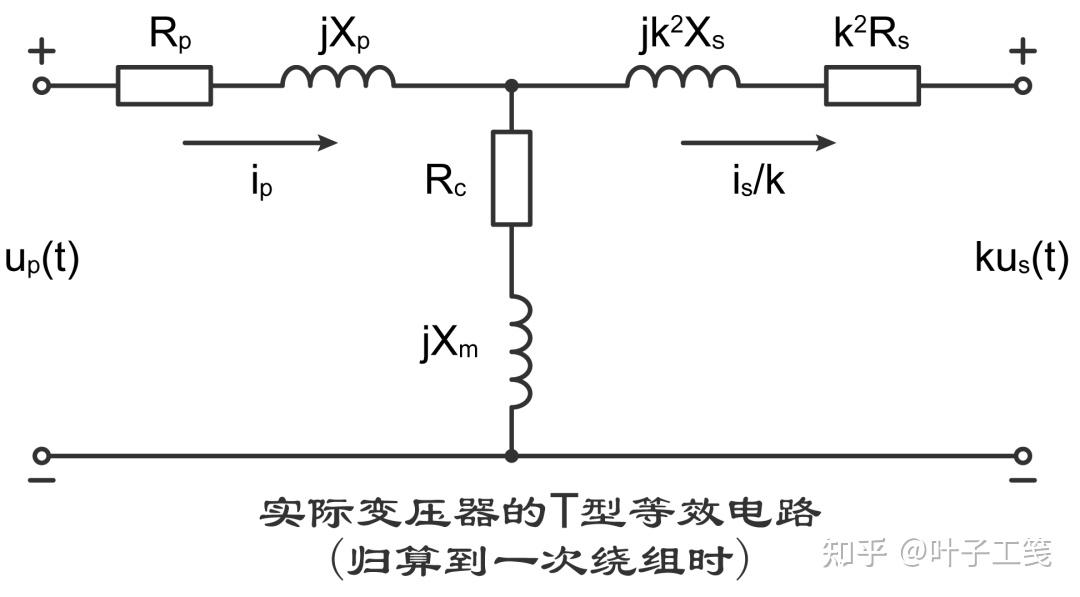
如果将二次绕组归算到一次绕组，实际变压器的等效电路就变为：

如果将一次绕组归算到二次绕组，实际变压器的等效电路将变为：

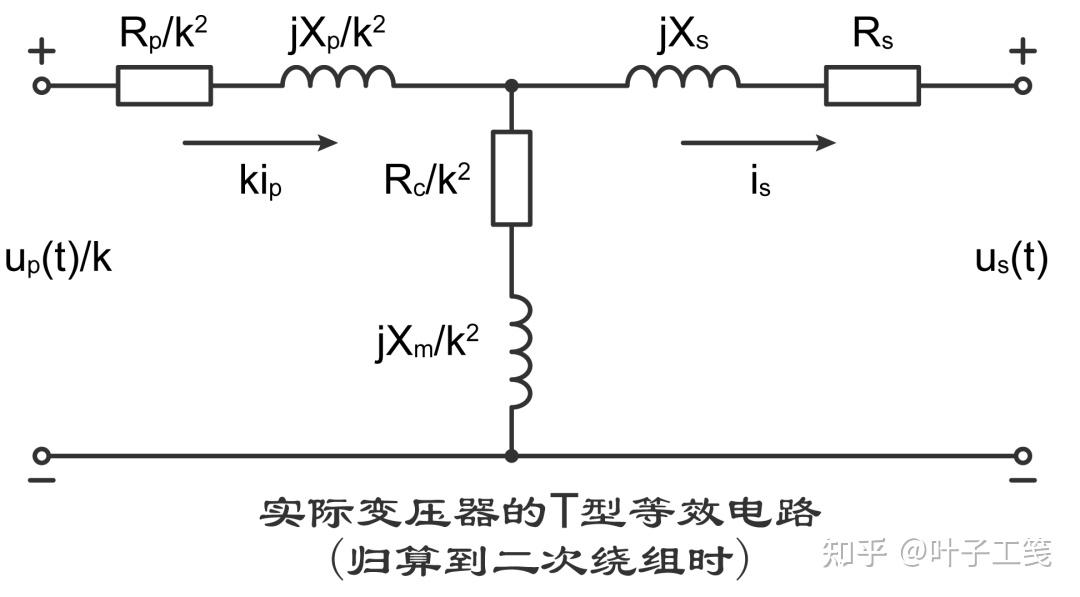
由于这两个电路的形状与字母 “T” 很相似，国内一般将它们称为 T形等效电路。