实际变压器等效电路中的参数测定

实际变压器可以转换为一个由理想变压器和等效元器件组成的等效电路。等效电路中的电阻和电抗可以使用试验方法测定。

开路试验

开路试验也叫空载试验，可以用来测定变压器的铁芯产生的铁芯损耗和磁阻在等效电路中的等效阻抗（即激磁阻抗）。

进行开路试验时，变压器中的一个绕组保持开路，在另一个绕组上施加额定电压。使用电流表、电压表和功率计分别测量变压器的输入电流、输入电压和输入功率。

为了试验安全和测量方便，进行开路试验时通常在低压侧施加电压。开路试验的接线图如下：

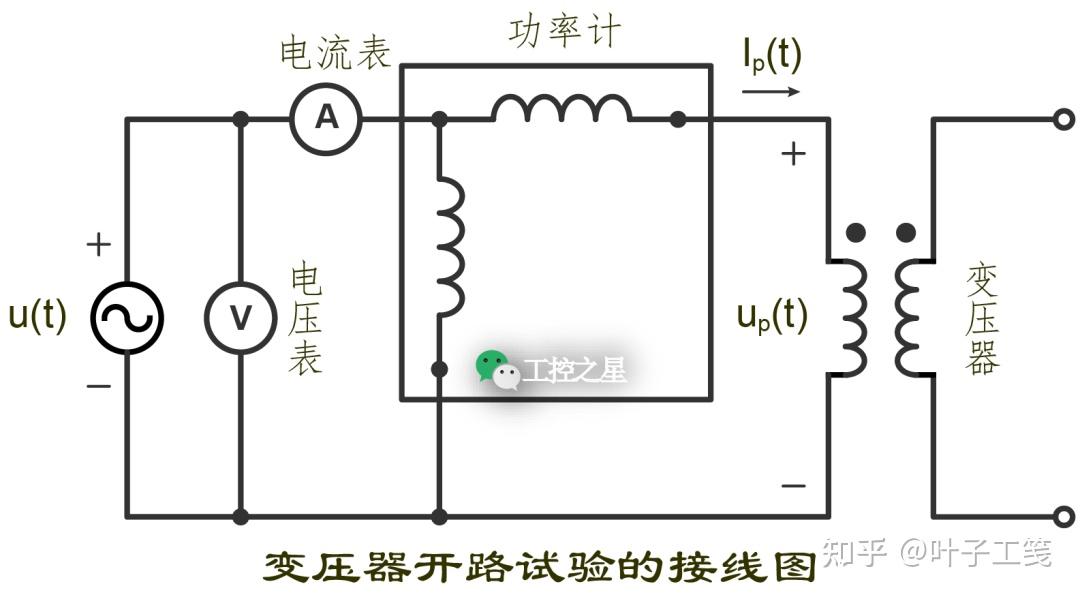
在 T形等效电路中，一次绕组上的铜损等效为电阻 \(R_{p}\)，一次绕组的漏磁通等效为电抗 \(X_{p}\)。\(R_{p}\) 和 \(X_{p}\) 合称为一次绕组的漏阻抗。

由于一次绕组的漏阻抗远远小于激磁阻抗 (\(Z_{e}\))，如果将其忽略不计，电压表测量的电压 (\(U_{oc}\)) 就是激磁支路两端的电压，电流表测量的电流 (\(I_{oc}\)) 就是激磁支路中的电流。

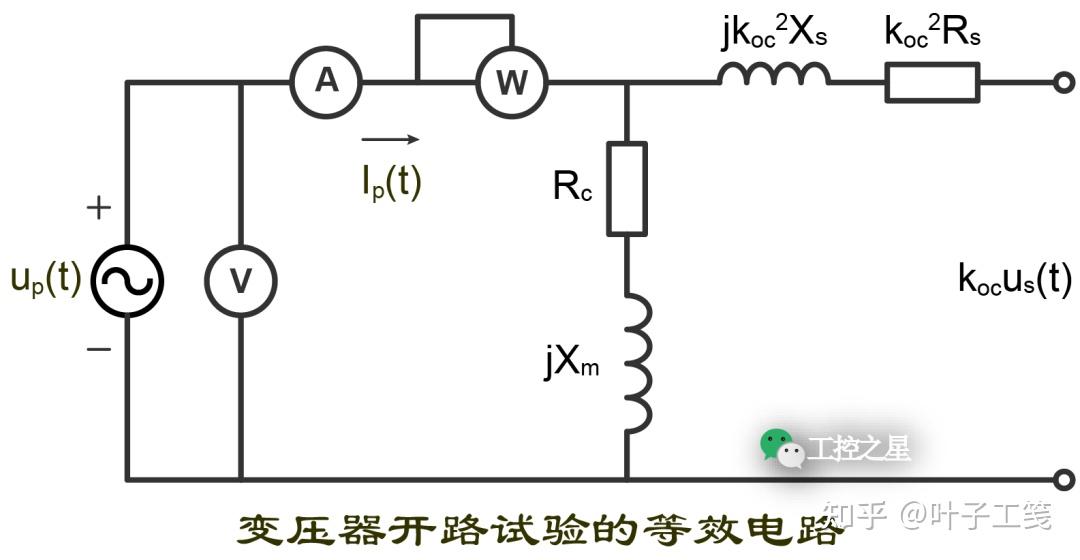
因此，激磁阻抗的模可以计算如下：

\[ |Z_e| = \frac{U_{oc}}{I_{oc}} \]

同理，功率计上显示的功率 (\(P_{oc}\)) 等于励磁支路上的有功功率。根据功率因数的计算公式，可得：

\[ \begin{align*} \cos{\theta} &= \frac{P_{oc}}{U_{oc}I_{oc}} \\ \theta &= \cos^{-1} \frac{P_{oc}}{U_{oc}I_{oc}} \end{align*} \]

由于变压器的激磁阻抗属于感性阻抗，电流的相位角滞后于电压的相位角。也就是说，激磁阻抗的相位角是正值，即：

\[ \begin{align*} Z_e &= \frac{U_{oc}}{I_{oc}} \angle{\theta} \\ &= \frac{U_{oc}}{I_{oc}} \angle{\cos^{-1} \frac{P_{oc}}{U_{oc}I_{oc}}} \end{align*} \]

因此，激磁支路上的电阻和电抗可以计算如下：

\[ \begin{align*} R_c &= |Z_e| \cos{\theta} \\ &= \frac{U_{oc}}{I_{oc}} \times \frac{P_{oc}}{U_{oc}I_{oc}} \\ &= \frac{P_{oc}}{I_{oc}^{2}} \\ X_m &= \sqrt{|Z_e|^2 - R_c^2} \end{align*} \]

由于电压施加在低压侧，上述计算结果为低压侧的归算值。

短路试验

短路试验也叫负载试验，可以用来测定变压器的一次绕组和二次绕组产生的铜损和漏磁通在等效电路中的等效阻抗（即一次绕组的漏阻抗和二次绕组的漏阻抗）。

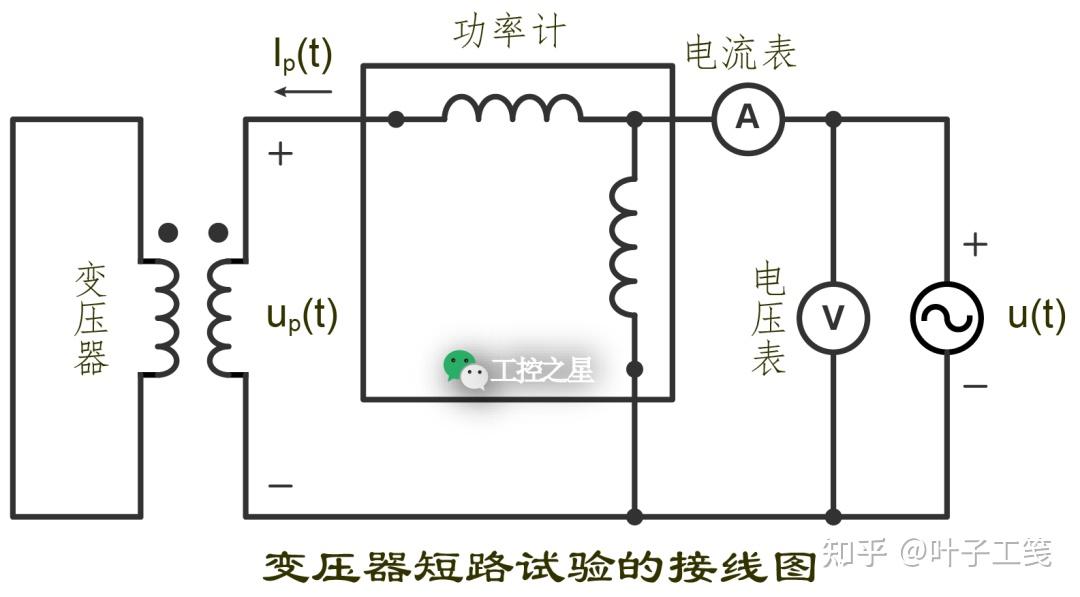
进行短路试验时，将变压器中的一个绕组短路，在另一个绕组上施加一个可变电压。调节可变电压，使短路电流的大小等于额定电流。使用电流表、电压表和功率计分别测量变压器的输入电流，输入电压和输入功率。

调节可变电压时，一定要确保电压大小处于安全范围内，以防变压器的绕组被烧坏。

为了试验安全和测量方便，进行短路试验时通常在高压侧施加电压。短路试验的接线图如下：

在短路试验中，输入电压很低。当短路电流为额定电流时，输入电压的大小一般只有额定电压的 5%~15%。因此，激磁支路上的电流也特别小。

如果将激磁支路上的电流忽略不计，短路试验的等效电路就变成了一个简化等效电路。电压表测量出的电压等于两个绕组的漏阻抗上的电压之和，电流表测量出的电流等于漏阻抗中流过的电流。

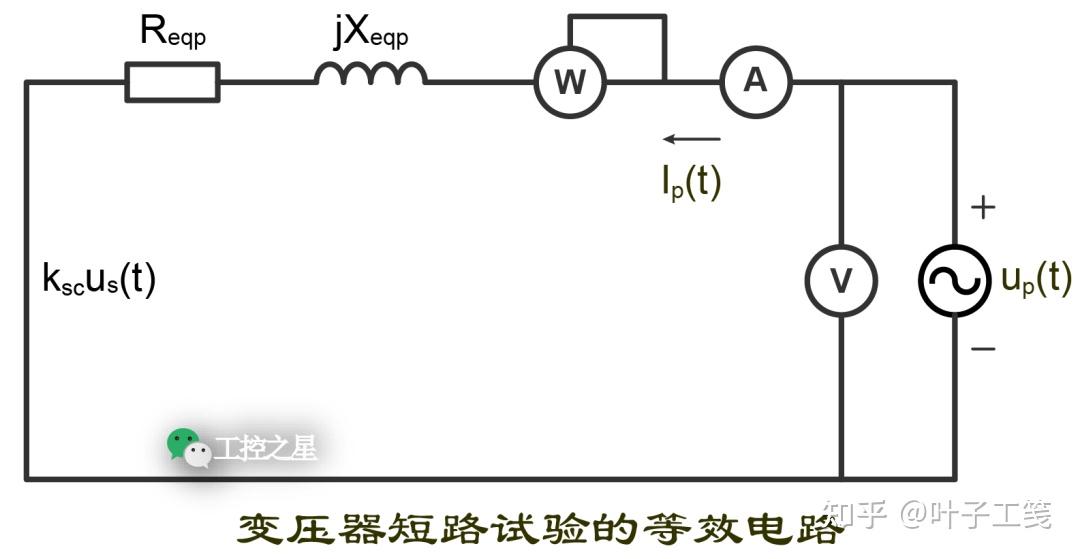
假设两个绕组的漏阻抗之和为 \(Z_{eqp}\)，即：

\[ \begin{align*} Z_{eqp} &= (R_p + jX_p) + k_{sc}^2(R_s + jX_s) \\ &= (R_p + k_{sc}^2R_s) + j(X_p + k_{sc}^2X_s) \\ &= R_{eqp} + jX_{eqp} \end{align*} \]

则 \(Z_{eqp}\) 的模可以计算如下：

\[ |Z_{eqp}| = \frac{U_{sc}}{I_{sc}} \]

同理，功率计上显示的功率 (\(P_{sc}\)) 等于两个绕组的漏阻抗上消耗的有功功率之和。根据功率因数的计算公式，可得：

\[ \begin{align*} \cos{\theta} &= \frac{P_{sc}}{U_{sc}I_{sc}} \\ \theta &= \cos^{-1} \frac{P_{sc}}{U_{sc}I_{sc}} \end{align*} \]

由于变压器的漏阻抗属于感性阻抗，电流的相位角滞后于电压的相位角。也就是说，漏阻抗的相位角是正值，即：

\[ \begin{align*} Z_{eqp} &= \frac{U_{sc}}{I_{sc}} \angle{\theta} \\ &= \frac{U_{sc}}{I_{sc}} \angle{\cos^{-1} \frac{P_{sc}}{U_{sc}I_{sc}}} \end{align*} \]

因此，变压器两个绕组上的总电阻和总电抗可以计算如下：

\[ \begin{align*} R_{eqp} &= R_p + k_{sc}^2R_s \\ &= |Z_{se}| \cos{\theta} \\ &= \frac{U_{sc}}{I_{sc}} \times \frac{P_{sc}}{U_{sc}I_{sc}} \\ &= \frac{P_{sc}}{I_{sc}^{2}} \\ X_{eqp} &= \sqrt{|Z_{se}|^2 - R_{eqp}^2} \end{align*} \]

使用上述方法计算出的漏阻抗是一次绕组的漏阻抗和二次绕组的漏阻抗之和。在实际应用中，大多使用近似等效电路或简化等效电路，没有必要分别计算出两个绕组的漏阻抗。如果必须使用 T 型等效电路，通常假设两个绕组的漏阻抗相等。

将变压器的漏磁场分为一次绕组的漏磁场和二次绕组的漏磁场，只是为了简化分析过程。实际上，变压器的漏磁场分布十分复杂，根本无法区分各个绕组的漏磁场，更无法准确测定各个绕组的漏阻抗。

由于电压施加在高压侧，上述计算结果为高压侧的归算值。

绕组归算

在开路试验中，施加电压的是变压器的低压侧，测定结果是激磁支路的阻抗和电抗在低压侧的归算值。

在短路试验中，施加电压的是变压器的高压侧，测定结果是两个绕组的总电阻和总电抗在高压侧的归算值。

显然，要画出一副完整的等效电路就必须将这两个试验中获得的测定结果归算到同一侧。

如果全部归算到高压侧，就将开路试验中得到的激磁阻抗乘以 \(k_{oc}^2\)。如果全部归算到低压侧，就将短路试验中得到的两个绕组的漏阻抗之和乘以 \(k_{sc}^2\)。

其中，开路试验中变压器的匝数比 (\(k_{oc}\)) 和短路试验中变压器的匝数比 (\(k_{sc}\)) 互为倒数，即：

\[ k_{oc} =\dfrac{1}{k_{sc}} \]