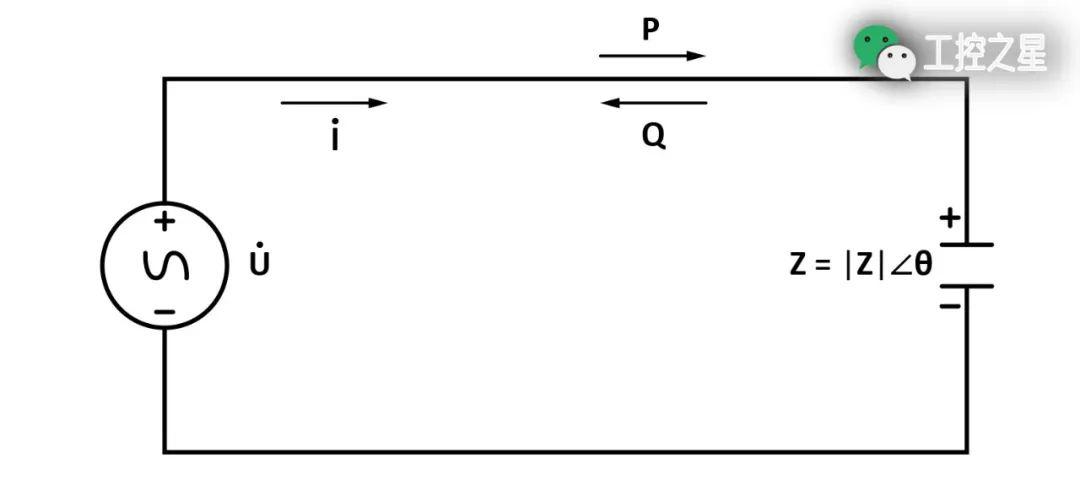
有功功率、无功功率和视在功率之间的关系

有功功率、无功功率和视在功率的概念比较抽象，使用三角函数计算起来也比较复杂。

为了便于理解和计算，人们经常使用复数和功率三角形来表示三者之间的关系。

与复阻抗的关系

在正弦交流电路中，如果一个负载的阻抗 (Z = |Z|∠θ) 是定值，负载两端的电压大小可以根据欧姆定律计算如下：

\[ U = I|Z| \]

其中，Z 是一个复阻抗，|Z| 是该复阻抗的模，θ 是该复阻抗的辐角。

将上式代入有功功率、无功功率和视在功率的计算公式，可得：

\[ \begin{align*} P &= UI \cos{\theta} \\ &= I^2|Z| \cos{\theta} \\ Q &= UI \sin{\theta} \\ &= I^2|Z| \sin{\theta} \\ S &= UI \\ &= I^2|Z| \end{align*} \]

Z = |Z|∠θ 是复阻抗的极坐标表示法。复阻抗还可以使用复数的一般形式表示如下：

\[ \begin{align*} Z &= R + jX \\ &= |Z| \cos{\theta} + j|Z|\sin{\theta} \end{align*} \]

即：

\[ \begin{align*} R &= |Z| \cos{\theta} \\ X &= |Z| \sin{\theta} \end{align*} \]

其中，复阻抗的实部 R 叫做有功电阻，复阻抗的虚部 X 叫做电抗。

提示

通常，电抗为正数时叫做感抗，电抗为负数时叫做容抗。

因此，有功功率和无功功率的计算公式还可以写为：

\[ \begin{align*} P &= I^2|Z| \cos{\theta} \\ &= I^2R \\ Q &= I^2|Z| \sin{\theta} \\ &= I^2X \end{align*} \]

与复功率的关系

在正弦交流电路中，电压和电流也可以使用复数表示。

\[ \begin{align*} \dot{U} &= U \angle{\alpha} \\ \dot{I} &= I \angle{\beta} \\ \end{align*} \]

这种用复数表示的正弦电压和正弦电流，分别叫做电压相量和电流相量。其中，正弦电压或正弦电流的有效值 (U 或 I) 是相量的模，正弦电压或正弦电流的初相角 (α 或 β) 是相量的辐角。

以相量法分析正弦交流将路时，经常用到的一个叫做复功率的辅助计算量。复功率 (\(\widetilde{S}\)) 是指电压相量与电流相量的共轭复数的乘积：

\[ \begin{align*} \widetilde{S} &= \dot{U} \dot{I}^* \\ &= (U\angle{\alpha})(I\angle{-\beta}) \\ &= UI\angle{(\alpha - \beta)} \\ &= UI\cos{(\alpha - \beta)} + jUI\sin{(\alpha - \beta)} \end{align*} \]

提示

上式中的星号 (*) 是复共扼运算符。

假设正弦电压和正弦电流的相位差是 θ （即 θ = α - β），那么上式可以变换为：

\[ \begin{align*} \widetilde{S} &= UI\cos{\theta} + jUI\sin{\theta} \\ &= P + jQ \end{align*} \]

也就是说，在正弦交流电路中，复功率的实部是有功功率 (P)，复功率的虚部是无功功率 (Q)，复功率的模是视在功率 (S = UI)。

功率三角形

有功功率、无功功率和视在功率之间的关系还可以使用功率三角形来表示。

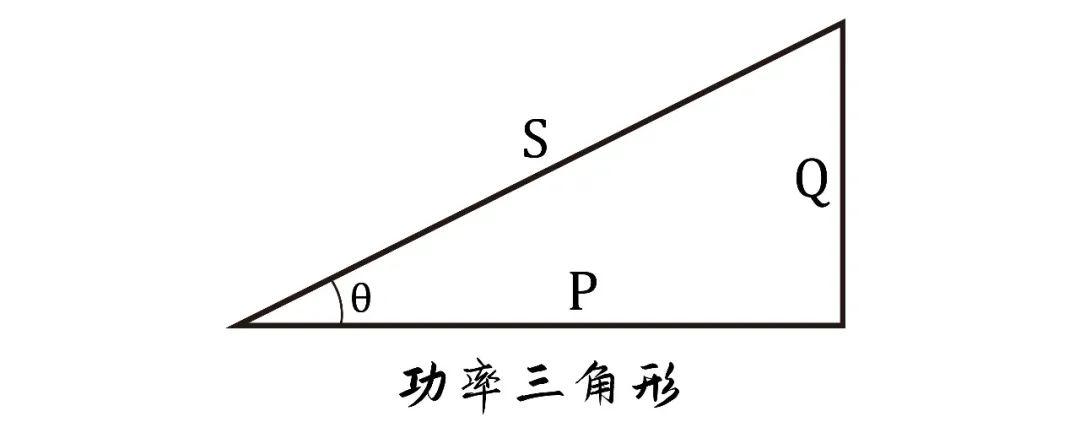
功率三角形左侧的锐角表示正弦电压和正弦电流之间的相位差 (θ)，底边表示有功功率 (P)，右侧边表示无功功率 (Q)，斜边表示视在功率 (S)。

通常，我们将 cosθ 称为功率因数。由功率三角形可知，功率因数等于有功功率与视在功率的比值。

\[ \cos{\theta = \frac{P}{S}} \]

注意一下，我们不能根据功率因数判断一个电路中的负载是感性负载还是容性负载，因为余弦函数是偶函数，即 cosθ = cos(-θ)。例如，一个电路的功率因数是 1/2，那么这个电路中的负载既有可能是感性负载（阻抗角为 +60°），也有可能是容性负载（阻抗角为 -60°）。

所以，在提到功率因数时，大家一般都会说明一下电路中的电流是超前于电压，还是滞后于电压。

物理意义

介绍有功功率、无功功率和视在功率时，已经提到过阻抗角的正负、电流与电压的相位差以及无功功率的物理意义了。现在我们再总结一下：

根据复数形式的欧姆定律，负载中的电流相量可计算如下：

\[ \begin{align*} \dot{I} &= \frac{\dot{U}}{Z} \\ &= \frac{U\angle{0^\circ}}{|Z|\angle{\theta}} \\ &= \frac{U}{|Z|}\angle{-\theta} \end{align*} \]

感性负载的电抗是正值（即感抗），阻抗角是正值，消耗的无功功率也是正值，其电流的相位角滞后于电压的相位角。感性负载既消耗电源的有功功率，也消耗电源的无功功率。

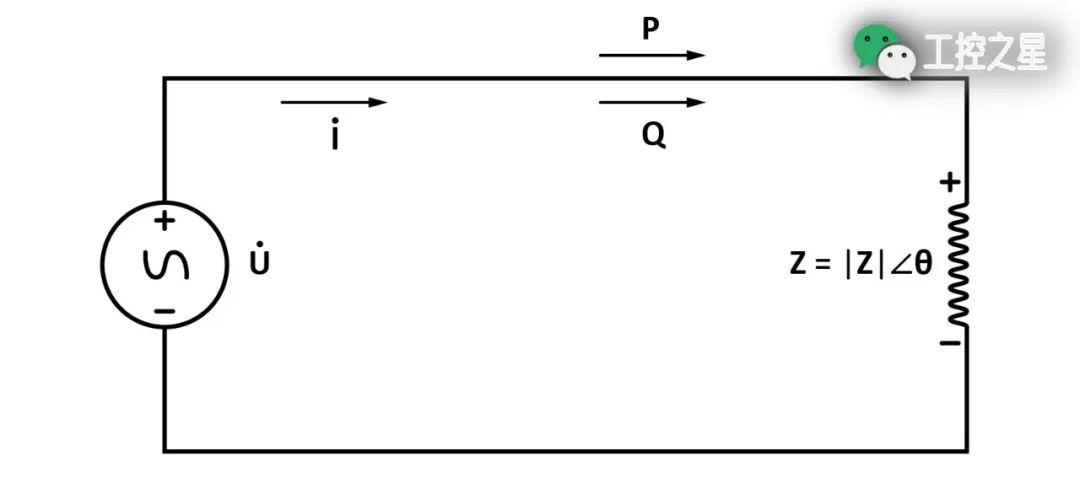
容性负载的电抗是负值（即容抗），阻抗角是负值，消耗的无功功率也是负值，其电流的相位角超前于电压的相位角。容性负载消耗电源的有功功率，返还给电源无功功率。