单相交流电路中的有功功率、无功功率和视在功率

我们的日常用电，不管是生活用电还是工业用电，基本都是正弦交流电。即使有些地方用的是直流电，那也是通过整流设备将正弦交流电转换成的直流电。

正弦交流电之所以这么普遍，是因为利用变压器就可以随意调整它的电压，便捷又经济。

在直流电路中，功率是用来表示电流做功快慢的物理量。功率的值等于电压与电流的乘积。

\[ P = UI \]

在正弦交流电路中，电压与电流之间有可能存在相位差。二者之间的相位差，不影响瞬时功率的计算，但却影响平均功率的计算。

所以，我们有必要好好研究一下正弦交流电路中的“功率家族”。

瞬时功率

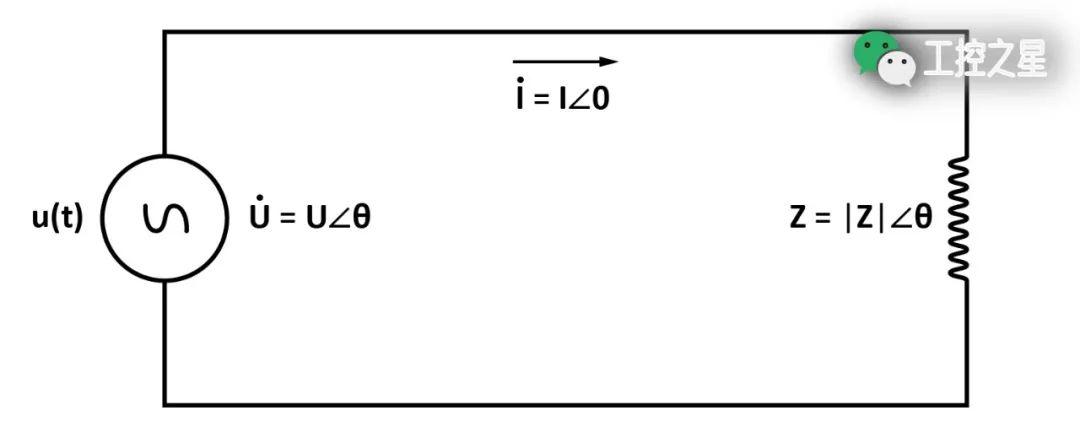
上图是一个单相的正弦交流电路，电路中有一个单相的阻抗 (Z = |Z|∠θ)，其阻抗角为 θ。

假设该阻抗是一个感性负载，根据电感电路中电压和电流的相位关系可知，阻抗角 θ 为正值，电路中的电流滞后于阻抗两端的电压 θ 度。

假设该电路中的瞬时电流表达式和瞬时电压表达式如下：

\[ \begin{align*} i(t) &= \sqrt{2} I \sin{\omega t} \\ u(t) &= \sqrt{2} U sin{(\omega t + \theta)} \end{align*} \]

其中， I 是该电路中电流的有效值，U 是阻抗两端电压的有效值。

交流电路中瞬时功率的计算方法，与直流电路的电功率计算方法相同。因此，该电路中的瞬时功率为计算如下：

\[ \begin{align*} p(t) &= u(t)i(t) \\ &= 2UIsin{\omega t} \sin{(\omega t + \theta)} \\ \end{align*} \]

经三角变换后，可得：

\[ p(t) = UI \cos{\theta}(1 - \cos{2 \omega t}) + UI \sin{\theta} \sin{2 \omega t} \]

在上面的公式中，第一项表示与电压同相的电流所做的功，第二项表示与电压有 90° 相位差的电流所做的功。

有功功率

在瞬时功率的计算公式中，有两个单项式。其中，第一个单项式永远是正数，且为周期函数。如果以时间 (t) 为横坐标、第一个单项式的函数值为纵坐标作图，可得到以下曲线：

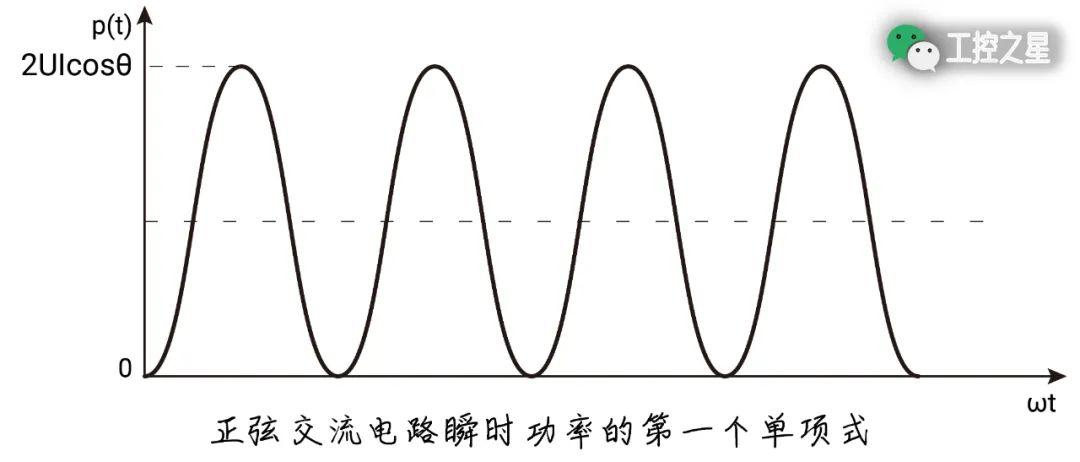
该曲线函数的平均值，叫做平均功率或有功功率 (P)。有功功率表示的是，正弦交流电路的电流中与电压同相位的那部分电流所做的功。

有功功率的计算公式如下：

\[ P = UI\cos{\theta} \]

有功功率的单位是瓦特 (W)。

无功功率

在瞬时功率的计算公式中，第二个单项式的函数值也是周期函数。如果以时间 (t) 为横坐标、第二个单项式的函数值为纵坐标作图，可得到以下曲线：

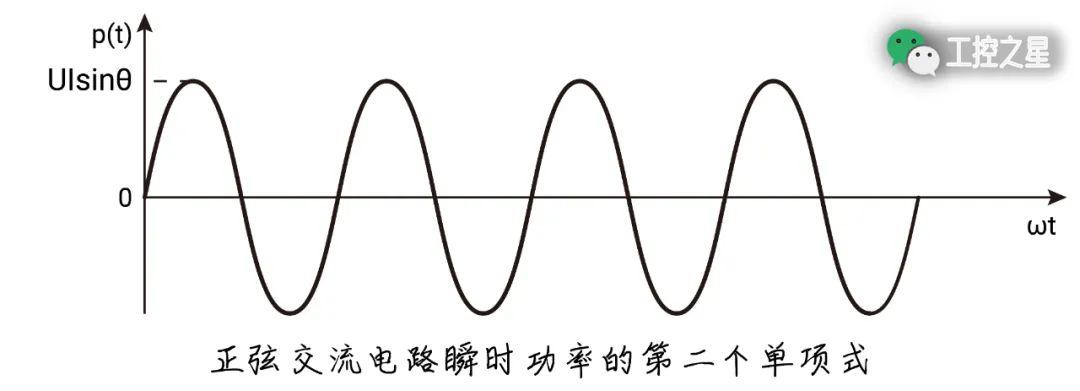
从图中可以看出，有半个周期的函数值是正的，另外半个周期的函数值是负的，且该曲线函数的平均值为零。

该曲线函数表示的是，正弦交流电路的电流中与电压有 90° 相位差的那部分电流所做的功。该曲线函数的最大值，叫做无功功率 (Q)。

无功功率的计算公式如下：

\[ Q = UI\sin{\theta} \]

无功功率表示的是，在电源和负载之间来回穿梭的能量。这部分能量先从电源流向负载，负载将这部分能量储存起来。等储存到一定程度之后，负载又将刚刚储存的能量逐渐释放出来，流回电源。之后，循环往复……

提示

如果是感性负载，无功功率表示的能量会被转换成磁能储存在负载中。流回电源前，负载会将储存的磁能转换回电能。

按照惯例，感性负载的阻抗角是正值，其无功功率也是正值；容性负载的阻抗角是负值，其无功功率也是负值。

无功功率的单位是乏 (var)。乏的量纲与瓦特完全相同，单独命名只是为了区分无功功率和一般功率。

视在功率

在正弦交流电路中，还有一个术语叫视在功率。视在功率 (S) 是交流电路中负载两端的电压有效值与负载中的电流有效值的乘积。

视在功率的计算公式如下：

\[ S = UI \]

视在功率的单位是伏·安 (VA)。伏·安、瓦特和乏的量纲完全相同，单独命名只是为了区分视在功率、无功功率和一般功率。