直线直流发电机的工作原理

上一节演示了直线直流电动机的工作过程。只要向直线直流电机简易模型中的导电棒上施加一个外力，且外力方向与其运动方向相反，简易模型就变成电动机了。

如果外力方向与运动方向相同，会怎么样呢?

简易模型启动完成后

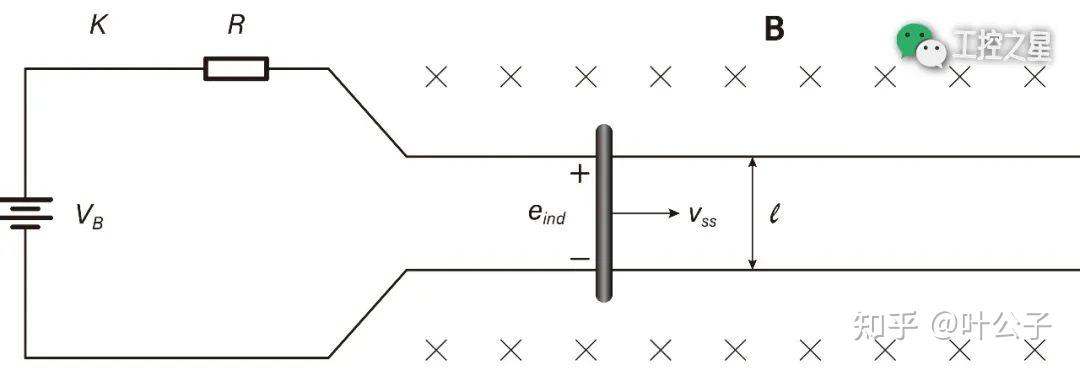
在直线直流电机简易模型中，有一组电池、一个电阻和一对儿绝对光滑的导轨。导轨上平放着一根金属导电棒。导轨的周围分布着均匀的恒磁场，方向垂直于屏幕向里。

电池、电阻、导轨、导电棒和开关组成了一个电路。开关一闭合，简易模型就启动了。

启动过程完成后，导电棒以速度 v_ss 向右保持匀速直线运动，并由此产生了一个与电源电压大小相同、方向相反的感应电动势 (e_ind)。这时，导电棒处于平衡状态（受力为零），电路中也没有电流。

\[ \begin{align*} v_{ss} &= \frac{V_B}{Bl} \\ e_{ind} &= V_B \\ F_{net} &= F_{ind} = 0 \\ i &= 0 \end{align*} \]

外力引起的运动状态变化

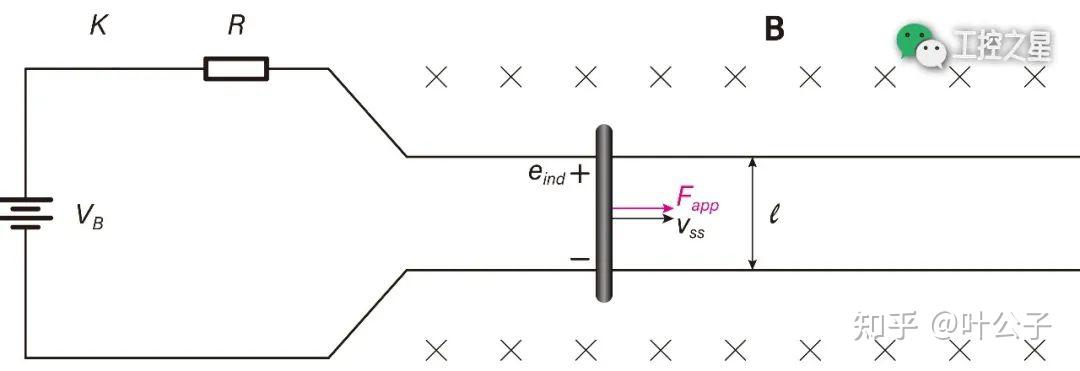
简易模型启动完成后，导电棒突然受到一个水平向右（与其运动方向相同）的外力 (F_app)，如图所示。

根据牛顿第二定律，导电棒在外力的作用下将产生水平向右的加速度，从而使移动速度（v）加快。

\[ F_{net} = F_{app} = ma \]

根据感生电动势的计算公式，导电棒的移动速度 (v) 加快了，导电棒上的感应电动势 (e_ind) 就会随之增大。

\[ \overset {\uparrow} e_{ind} = \overset {\uparrow} vBl \]

由于向导电棒施加外力前，感应电动势与电源电压大小相等、方向相反。根据基尔霍夫电压定律，施加外力之后导电棒上的感应电动势增大了（e_ind > V_B），电路中就会产生与电源电压方向相反的电流（反向电流），其大小会随着感应电动势的增加而增加。

\[ \begin{align*} \overset {\uparrow} i = \frac{\overset {\uparrow} e_{ind} - V_B}{R} & \end{align*} \]

由于产生了反向电流（沿导电棒方向向上），根据左手定则和安培力的计算公式，磁场就向导电棒施加向左的安培力，且随着电流的增大而增大。

\[ \begin{align} \overset {\uparrow} F_{ind} = \overset {\uparrow} ilB \end{align} \]

当导电棒受到的安培力增大到与外力大小相等时，导电棒达到平衡状态，即导电棒又恢复到匀速直线运动状态了。只是，导电棒的运动速度相比之前加快了一些。

发电机的工作原理

上文中简易模型的运动状态变化过程，其实就是直线直流发电机的工作过程：

在发电机的主轴上施加一个扭矩，扭矩的方向与主轴的运动方向相反。这时，主轴的转速就会增加。主轴的转速增加了，线圈中的感应电动势就会增大。线圈中的感应电动势增大了，线圈中就会产生反方向的电流并不断增大，为电池（负载）充电。

如此以来，发电机就实现了从机械能到电能的转换。转换方程如下：

\[ P_{conv} = F_{ind}v \]

如果以角速度表示的话，转换方程还可以写为：

\[ P_{conv} = \tau_{ind}\omega \]

其中，τ_ind 是安培力 F_ind 在旋转运动中的对应物理量，角速度 ω 是速率 v 在旋转运动中的对应物理量。

总结

同一台电机，既可以用作电动机，也可以用作发电机。唯一的区别是，外力施加的方向不同。

从电学上来说，当感应电动势小于电源电压 (e_ind < V_B) 时，电机被用作电动机；当感应电动势大于电源电压 (e_ind > V_B)时，电机被用作发电机。

无论用作电动机还是发电机，电机中都会产生安培力和感应电动势。区别只在于，外力施加的方向不同（相对于主轴的运动方向）。

从运动学上来说，当主轴的转速减慢了时，电机被用作电动机；当主轴的转速加快了时，电机被用作发电机。

无论用作电动机还是发电机，电机主轴的转动方向都是相同的。不过，电流方向是相反的。

提示

经常有初学者误以为，电动机和发电机的主轴转动方向是相反的。但其实，它们只是一个转得快一点、一个转得慢一点而已。